
设关于x函数 其中0
其中0
将f(x)的最小值m表示成a的函数m=g(a);
是否存在实数a,使f(x)>0在 上恒成立?
上恒成立?
是否存在实数a,使函数f(x) 在 上单调递增?若存在,写出所有的a组成的集合;若不存在,说明理由.
上单调递增?若存在,写出所有的a组成的集合;若不存在,说明理由.
科目:高中数学 来源: 题型:解答题
已知函数f(x)=xk+b(其中k,b∈R且k,b为常数)的图象经过A(4,2)、B(16,4)两点.
(1)求f(x)的解析式;
(2)如果函数g(x)与f(x)的图象关于直线y=x对称,解关于x的不等式:g(x)+g(x-2)>2a(x-2)+4.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了寻找马航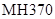 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线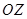 方向航行,而在港口北偏东
方向航行,而在港口北偏东 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
,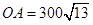 海里,且
海里,且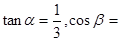
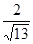 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口 正东
正东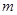 海里的
海里的 处的补给船,速往小岛
处的补给船,速往小岛 装上补给物资供给科考船.该船沿
装上补给物资供给科考船.该船沿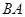 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线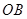 围成的三角形
围成的三角形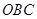 的面积
的面积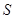 最小时,这种补给方案最优.
最小时,这种补给方案最优.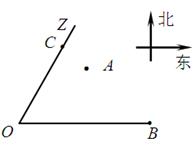
(1)求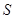 关于
关于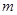 的函数关系式
的函数关系式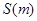 ;
;
(2)应征调位于港口正东多少海里处的补给船只,补给方案最优?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
椭圆c: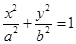 (a>b>0)的离心率为
(a>b>0)的离心率为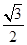 ,过其右焦点F与长轴垂直的弦长为1,
,过其右焦点F与长轴垂直的弦长为1,
(1)求椭圆C的方程;
(2)设椭圆C的左右顶点分别为A,B,点P是直线x=1上的动点,直线PA与椭圆的另一个交点为M,直线PB与椭圆的另一个交点为N,求证:直线MN经过一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD、AB距离分别为9m、3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN∶NE=16∶9.线段MN必须过点P,端点M、N分别在边AD、AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
(1)用x的代数式表示AM;
(2)求S关于x的函数关系式及该函数的定义域;
(3)当x取何值时,液晶广告屏幕MNEF的面积S最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设f(x)=loga(1+x)+loga(3-x)(a>0,a≠1),且f(1)=2.
(1)求a的值及f(x)的定义域.
(2)求f(x)在区间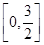 上的最大值.
上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com