
设f(x)=loga(1+x)+loga(3-x)(a>0,a≠1),且f(1)=2.
(1)求a的值及f(x)的定义域.
(2)求f(x)在区间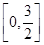 上的最大值.
上的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
某地需要修建一条大型输油管道通过240公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为400万元,铺设距离为 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为 万元.设余下工程的总费用为
万元.设余下工程的总费用为 万元.
万元.
(1)试将 表示成
表示成 的函数;
的函数;
(2)需要修建多少个增压站才能使 最小,其最小值为多少?
最小,其最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 ,
, ,
,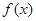 的最小值为
的最小值为 .
.
⑴求函数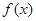 的解析式;
的解析式;
⑵设 ,若
,若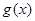 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
⑶设函数 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)的图象与函数h(x)=x+ +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+ ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数
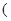 常数
常数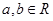 )满足
)满足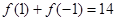 .
.
(1)求出 的值,并就常数
的值,并就常数 的不同取值讨论函数
的不同取值讨论函数 奇偶性;
奇偶性;
(2)若 在区间
在区间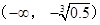 上单调递减,求
上单调递减,求 的最小值;
的最小值;
(3)在(2)的条件下,当 取最小值时,证明:
取最小值时,证明: 恰有一个零点
恰有一个零点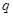 且存在递增的正整数数列
且存在递增的正整数数列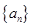 ,使得
,使得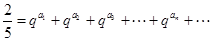 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设关于x函数 其中0
其中0
将f(x)的最小值m表示成a的函数m=g(a);
是否存在实数a,使f(x)>0在 上恒成立?
上恒成立?
是否存在实数a,使函数f(x) 在 上单调递增?若存在,写出所有的a组成的集合;若不存在,说明理由.
上单调递增?若存在,写出所有的a组成的集合;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com