
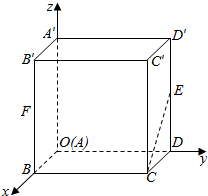
 如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离.
如图,空间直角坐标系中由长方体ABCD-A′B′C′D′,AB=1,BC=2,AA′=2,E和F分别是棱DD′和BB′的中点.证明:CE∥A′F,并求它们之间的距离. 分析 求出点的坐标,可得$\overrightarrow{CE}$=-$\overrightarrow{A′F}$,即可证明CE∥A′F,利用平面A′B与平面D′C的距离为2,可得CE与A′F之间的距离.
解答 证明:由题意,A′(0,0,2),F(1,0,1),C(1,2,0),E(0,2,1),
∴$\overrightarrow{CE}$=(-1,0,1),$\overrightarrow{A′F}$=(1,0,-1),
∴$\overrightarrow{CE}$=-$\overrightarrow{A′F}$,
∴CE∥A′F,
∵平面A′B与平面D′C的距离为2,
∴CE与A′F之间的距离为2.
点评 本题考查向量知识的运用,考查学生的计算能力,正确求出向量的坐标是关键.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com