
| 1 |
| 2 |
| tanx-1 |
|
| 2 |
| 3 |
| π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |
|
|
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 3 |
| 4 |
| 7 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省丹东市宽甸二中高二下学期期末考试数学(理) 题型:解答题
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
.
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及
的分布列及 ;
;
(2)设 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数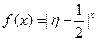 在定义域内单调递增”为事件
在定义域内单调递增”为事件 ,求事件
,求事件 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源:2011年福建省高二上学期期末考试数学理卷 题型:解答题
.(本小题满分13分)
银河科技有限公司遇到一个技术难题,隧紧急成立甲、乙两个攻关小组,按要求各自独立进行为期一月的技术攻关,同时决定在攻关期满对攻克难题的小组给予奖励,已知这些技术难题在攻关期满时被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 。
。
(I)设 为攻关期满时获奖小组的个数,求
为攻关期满时获奖小组的个数,求 的分布列;
的分布列;
(Ⅱ)设 为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递减“为事件
在定义域内单调递减“为事件 ,求事件
,求事件 发生的概率。
发生的概率。
查看答案和解析>>
科目:高中数学 来源:2012届辽宁省丹东市高二下学期期末考试数学(理) 题型:解答题
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
.
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及
的分布列及 ;
;
(2)设 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递增”为事件
在定义域内单调递增”为事件 ,求事件
,求事件 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com