
分析 由已知得:a3+a2=3,a5+a4=-5,…a2017+a2016=-2017,把以上各式相加得:S2017-a1=-1008,可得a1+b=1,又a1b>0,a1,b>0.再利用“乘1法”与基本不等式性质即可得出.
解答 解:由已知得:a3+a2=3,a5+a4=-5,…a2017+a2016=-2017,
把以上各式相加得:S2017-a1=-1008,
即:a1-1008=-1007-b,
∴a1+b=1,又a1b>0,
∴a1,b>0.
则$\frac{1}{a_1}+\frac{2}{b}$=(a1+b)$(\frac{1}{{a}_{1}}+\frac{2}{b})$=3+$\frac{b}{{a}_{1}}$+$\frac{2{a}_{1}}{b}$≥3+$2\sqrt{\frac{b}{{a}_{1}}•\frac{2{a}_{1}}{b}}$=3+2$\sqrt{2}$,当且仅当b=$\sqrt{2}$a1=2-$\sqrt{2}$时取等号.
故答案为:$3+2\sqrt{2}$.
点评 本题考查了“累加求和”、“乘1法”与基本不等式性质,考查了分类讨论方法、推理能力与就计算能力,属于中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
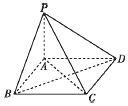
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 非上述三种图形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
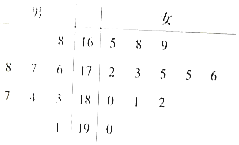 某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
某校开展运动会,招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
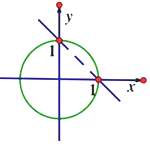
| A. | (x+y-1)•(x2+y2-1)=0 | B. | $\sqrt{x+y-1}•({x^2}+{y^2}-1)=0$ | ||
| C. | $(x+y-1)•\sqrt{{x^2}+{y^2}-1}=0$ | D. | $\sqrt{x+y-1}•\sqrt{{x^2}+{y^2}-1}=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 与教育有关 | 与教育无关 | 合计 | |
| 男 | 30 | 10 | 40 |
| 女 | 35 | 5 | 40 |
| 合计 | 65 | 15 | 80 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com