
思路解析:整个比赛采用五局三胜制,则至少比赛3局,至多比赛5局,因而随机变量ξ的可能取值为3、4、5,而每种情形均包括甲获胜与乙获胜两种可能.
解:单局比赛甲队胜乙队的概率为0.6,
乙队胜甲队的概率为1-0.6=0.4
比赛3局结束有两种情况:甲队胜3局或乙队胜3局,
因而P(ξ=3)=0.63+0.43=0.28
比赛4局结束有两种情况:前3局中甲队胜2局,第4局甲队胜;或前3局中乙队胜2局,第4局乙队胜。
因而P(ξ=4)=![]() ×0.62×0.4×0.6+
×0.62×0.4×0.6+![]() ×0.42×0.6×0.4=0.374 4.
×0.42×0.6×0.4=0.374 4.
比赛5局结束有两种情况:前4局中甲队胜2局、乙队胜2局,第5局甲胜或乙胜.
因而P(ξ=5)=![]() ×0.62×0.42×0.6+
×0.62×0.42×0.6+![]() ×0.42×0.62×0.4=0.345 6.
×0.42×0.62×0.4=0.345 6.
所以ξ的概率分布为
ξ | 3 | 4 | 5 |
P | 0.28 | 0.374 4 | 0.345 6 |
ξ的期望Eξ=3×P(ξ=3)+4×P(ξ=4)+5×P(ξ=5)=4.065 6.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(理)令ξ为本场比赛的局数,求ξ的概率分布和数学期望.(精确到0.000 1)?
(文)求(1)前三局比赛甲队领先的概率;?
(2)求本场比赛乙队以3∶2取胜的概率.(精确到0.001)
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高二第二学期期末考试数学(理)试题 题型:填空题
甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.5,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互之间没有影响.用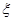 表示本场比赛的局数,则
表示本场比赛的局数,则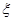 的数学期望为
▲ .
的数学期望为
▲ .
查看答案和解析>>
科目:高中数学 来源:河北省邯郸市2009-2010学年度高二第二学期期末教学质量检测 题型:解答题
(理科做)
甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响.令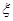 为本场比赛的局数.求
为本场比赛的局数.求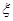 的概率分布和数学期望.(精确到0.0001)
的概率分布和数学期望.(精确到0.0001)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com