已知数列{an}中,a1=3,an+1-2 an=0,数列{bn}中,bn•an=(-1)n(n∈N*).
(Ⅰ)求数列{an}通项公式;
(Ⅱ)求数列{bn}通项公式以及前n项的和.
解(I)∵a
n+1-2a
n=0,∴
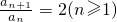
又∵a
1=3,∴{a
n}是首项为3,公比为2的等比数列,
∴a
n=3•2
n-1(n∈N
*)
(II)∵b
n•a
n=(-1)
n(n∈N
*)
∴
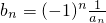
=
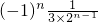
,
则{b
n}是以-

为公比,

为首项的等比数列,
∴S
n=b
1+b
2+…+b
n=
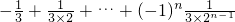
=
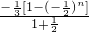
=-
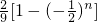
=
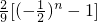
.
分析:(Ⅰ)根据递推公式判断出该数列是等比数列,求出公比,代入等比数列的通项公式求出;
(Ⅱ)根据题意和(Ⅰ)的结果,代入所给的式子求出{b
n}通项公式,判断出{b
n}是等比数列,代入前n项和公式进行求解.
点评:本题考点是等比数列的通项公式以及前n项和公式的应用,主要根据所给的式子进行变形,再由等比数列的定义进行判断.
