
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
(1) ;(2) ;(3)见解析.
【解析】
试题分析:(1)先记“甲以4比1获胜”为事件A,由题意甲乙一共比赛5局,则甲前4局比赛中有且只有3局获胜,第5局比赛一定获胜,易得甲以4比1获胜的概率为P(A)=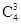 ()3·()4-3·= ;(2)同(1)中道理,“乙获胜且比赛局数多于5局”分两种情况:一是比赛6局,二是比赛7局,分别计算出概率再相加即得结论;(3)比赛的局数的可能值为4、5、6、7,分别计算取不同值时的概率,列表得分布列.
()3·()4-3·= ;(2)同(1)中道理,“乙获胜且比赛局数多于5局”分两种情况:一是比赛6局,二是比赛7局,分别计算出概率再相加即得结论;(3)比赛的局数的可能值为4、5、6、7,分别计算取不同值时的概率,列表得分布列.
试题解析:(1)由已知,甲、乙两名运动员在每一局比赛中获胜的概率都是. 1分
记“甲以4比1获胜”为事件A,则P(A)=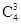 ()3·()4-3·=. 3分
()3·()4-3·=. 3分
(2)记“乙获胜且比赛局数多于5局”为事件B.
因为乙以4比2获胜的概率为P1=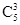
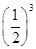 ·
·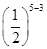 ·=,
·=,
乙以4比3获胜的概率为P2=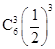 ·
·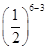 ·=,
·=,
所以P(B)=P1+P2=. 7分
(3)设比赛的局数位X,则X的可能取值为4,5,6,7. 8分
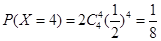 ,
,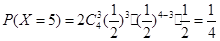 ,
,
 ,
,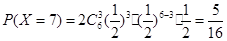 , 11分
, 11分
比赛局数的分布列为
|
X |
4 |
5 |
6 |
7 |
|
P |
|
|
|
|
考点:1、概率;2、概率分布列.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市西城区高三4月第一次模拟考试理科数学(解析版) 题型:填空题
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用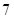 局
局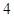 胜制(即先胜
胜制(即先胜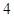 局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(Ⅰ)求甲以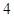 比
比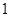 获胜的概率;
获胜的概率;
(Ⅱ)求乙获胜且比赛局数多于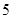 局的概率;
局的概率;
(Ⅲ)求比赛局数的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com