
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B,E,F,C四点共圆.
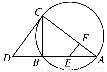
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值.
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集12讲练习卷(解析版) 题型:选择题
下面四个命题:
①“直线a∥直线b”的充分条件是“直线a平行于直线b所在的平面”;
②“直线l⊥平面α”的充要条件是“直线垂直平面α内无数条直线”;
③“直线a,b不相交”的必要不充分条件是“直线a,b为异面直线”;
④“平面α∥平面β”的必要不充分条件是“平面α内存在不共线三点到平面β的距离相等”.
其中为真命题的序号是( )
A.①② B.②③ C.③④ D.④
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲练习卷(解析版) 题型:解答题
设不等式|x-2|<a(a∈N*)的解集为A,且 ∈A,
∈A, ∉A.
∉A.
(1)求a的值;
(2)求函数f(x)=|x+a|+|x-2|的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷(解析版) 题型:解答题
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos 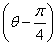 =2
=2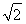 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷(解析版) 题型:填空题
曲线C的直角坐标方程为x2+y2-2x=0,以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A,B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD,CD.

(1)求证:BD平分∠CBE;
(2)求证:AH·BH=AE·HC.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题抢分训练练习卷(解析版) 题型:解答题
设L为曲线C:y=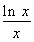 在点(1,0)处的切线.
在点(1,0)处的切线.
(1)求L的方程;
(2)证明:除切点(1,0)之外,曲线C在直线L的下方.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(四)第二章第一节练习卷(解析版) 题型:填空题
已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其函数对应关系如下表:

则方程g(f(x))=x的解集为____________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(八)第二章第五节练习卷(解析版) 题型:选择题
函数f(x)=1+log2x,f(x)与g(x)=21-x在同一直角坐标系下的图象大致是( )
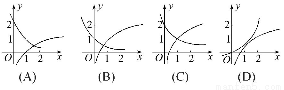
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com