
如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A,B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD,CD.

(1)求证:BD平分∠CBE;
(2)求证:AH·BH=AE·HC.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集11讲练习卷(解析版) 题型:解答题
如图所示,在四棱锥P-ABCD中,△PBC为正三角形,PA⊥底面ABCD,其三视图如图所示,俯视图是直角梯形.


(1)求正视图的面积;
(2)求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷(解析版) 题型:解答题
已知a,b为正实数.
(1)求证: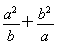 ≥a+b;
≥a+b;
(2)利用(1)的结论求函数y=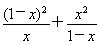 (0<x<1)的最小值.
(0<x<1)的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷(解析版) 题型:填空题
在极坐标系中,已知两圆C1:ρ=2cos θ和C2:ρ=2sin θ,则过两圆圆心的直线的极坐标方程是________________________________________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B,E,F,C四点共圆.
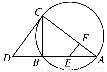
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题抢分训练练习卷(解析版) 题型:解答题
已知函数f(x)=(ax2-2x+a)·e-x.
(1)当a=1时,求函数f(x)的单调区间;
(2)设g(x)=-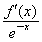 -a-2,h(x)=
-a-2,h(x)=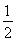 x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围.
x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
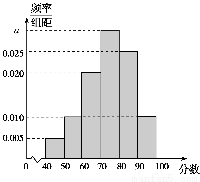
(1)求图中实数a的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(四)第二章第一节练习卷(解析版) 题型:选择题
如果f(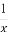 )=
)=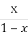 ,则当x≠0且x≠1时,f(x)=( )
,则当x≠0且x≠1时,f(x)=( )
(A)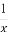 (B)
(B)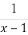 (C)
(C)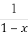 (D)
(D)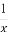 -1
-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com