
已知函数f(x)=(ax2-2x+a)·e-x.
(1)当a=1时,求函数f(x)的单调区间;
(2)设g(x)=-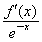 -a-2,h(x)=
-a-2,h(x)=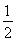 x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围.
x2-2x-ln x,若x>1时总有g(x)<h(x),求实数a的取值范围.
(1)单调递增区间为(1,3),单调递减区间为(-∞,1),(3,+∞).(2)-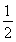 ≤a≤
≤a≤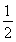
【解析】(1)当a=1时,函数f(x)=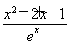 ,其定义域为R.
,其定义域为R.
f′(x)=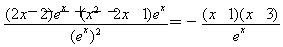
由f′(x)>0,得1<x<3,由f′(x)<0,得x<1或x>3,
∴函数f (x)的单调递增区间为(1,3),单调递减区间为(-∞,1),(3,+∞).
(2)∵f′(x)=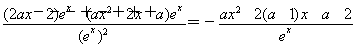 ,
,
∴g(x)=-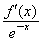 -a-2=ax2-2(a+1)x,
-a-2=ax2-2(a+1)x,
令φ(x)=g(x)-h(x)=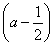 x2-2ax+ln x(x>1),
x2-2ax+ln x(x>1),
当x>1时总有g(x)<h(x)等价于φ(x)<0在(1,+∞)上恒成立.
φ′(x)=(2a-1)x-2a+ =
=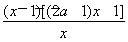 .
.
①若a>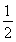 ,令φ′(x)=0得x1=1,x2=
,令φ′(x)=0得x1=1,x2=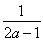 .
.
当x2>x1=1,即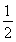 <a<1时,在(1,x2)上φ′(x)<0,则φ(x)单调递减;
<a<1时,在(1,x2)上φ′(x)<0,则φ(x)单调递减;
在(x2,+∞)上φ′(x)>0,则φ(x)单调递增.
故φ(x)的值域为[φ(x2),+∞),不合题意,舍去.
当x2≤x1=1,即a≥1时,同理可得φ(x)在(1,+∞)上单调递增,
故φ(x)的值域为(φ(1),+∞),不合题意,舍去.
②若a≤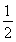 ,即2a-1≤0时,在区间(1,+∞)上恒有φ′(x)<0,则φ(x)单调递减,φ(x)<φ(1)=-a-
,即2a-1≤0时,在区间(1,+∞)上恒有φ′(x)<0,则φ(x)单调递减,φ(x)<φ(1)=-a-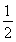 ≤0,
≤0,
∴-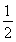 ≤a≤
≤a≤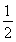


科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷(解析版) 题型:填空题
若对任意的a∈R,不等式|x|+|x-1|≥|1+a|-|1-a|恒成立,则实数x的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷(解析版) 题型:选择题
在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是( )
A. 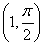 B.
B. 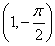 C.(1,0) D.(1,π)
C.(1,0) D.(1,π)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A,B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD,CD.

(1)求证:BD平分∠CBE;
(2)求证:AH·BH=AE·HC.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
如图,在几何体ABCDE中,AB=AD=2,AB⊥AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,且AE=MC= .
.
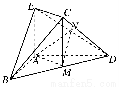
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如图.

(1)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格);
(2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为 1,
1, 2,估计
2,估计 1-
1- 2的值.
2的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(四)第二章第一节练习卷(解析版) 题型:选择题
下列各组函数中,表示同一函数的是( )
(A)y=1,y=
(B)y=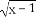 ·
·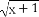 ,y=
,y=
(C)y=x,y=
(D)y=|x|,y=(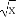 )2
)2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(五)第二章第二节练习卷(解析版) 题型:选择题
定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),当x<0时,f(x)>0,则函数f(x)在[a,b]上有( )
(A)最小值f(a) (B)最大值f(b)
(C)最小值f(b) (D)最大值f( )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com