
已知数列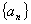 满足
满足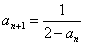 ,
,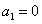 .
.
(1)计算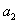 ,
,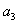 ,
,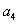 ,
,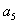 的值;
的值;
(2)根据以上计算结果猜想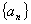 的通项公式,并用数学归纳法证明你的猜想.
的通项公式,并用数学归纳法证明你的猜想.
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
如图所示,一个类似杨辉三角的数阵,则第n(n≥2)行的第2个数为( )
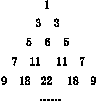
A.n2+2n+3 B.n2+2n-3
C.n2-2n+3 D.n2-2n-3
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax-bxln x,其图象经过点(1,1),且在点(e,f(e))处的切线斜率为3.(e为自然对数的底数).
(1)求实数a、b的值;
(2)若k∈Z,且k<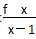 对任意x>1恒成立,求k的最大值;
对任意x>1恒成立,求k的最大值;
(3)证明:2ln 2+3ln 3+…+nln n>(n-1)2(n∈N*,n>1).
查看答案和解析>>
科目:高中数学 来源: 题型:
从装有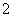 个白球和
个白球和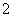 个蓝球的口袋中任取
个蓝球的口袋中任取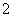 个球,那么对立的两个事件是( )
个球,那么对立的两个事件是( )
A.“恰有一个白球”与“恰有两个白球”
B.“至少有一个白球”与“至少有—个蓝球”
C.“至少有—个白球”与“都是蓝球”
D.“至少有一个白球”与“都是白球”
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知圆 外有一点
外有一点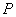 ,作圆
,作圆 的切线
的切线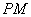 ,
,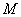 为切点,过
为切点,过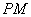 的中点
的中点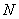 ,作割线
,作割线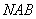 ,交圆于
,交圆于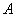 、
、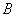 两点,连接
两点,连接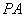 并延长,交圆
并延长,交圆 于点
于点 ,连接
,连接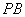 交圆
交圆 于点
于点 ,若
,若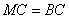 .
.
(1)求证:△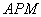 ∽△
∽△ ;
;
(2)求证:四边形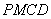 是平行四边形.
是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com