
如图所示,已知圆 外有一点
外有一点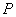 ,作圆
,作圆 的切线
的切线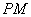 ,
,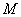 为切点,过
为切点,过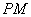 的中点
的中点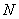 ,作割线
,作割线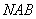 ,交圆于
,交圆于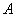 、
、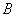 两点,连接
两点,连接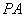 并延长,交圆
并延长,交圆 于点
于点 ,连接
,连接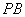 交圆
交圆 于点
于点 ,若
,若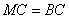 .
.
(1)求证:△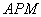 ∽△
∽△ ;
;
(2)求证:四边形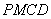 是平行四边形.
是平行四边形.

【解析】(1)见解析;(2)见解析
解析:(1)∵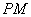 是圆
是圆 的切线,
的切线, 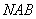 是圆
是圆 的割线,
的割线, 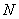 是
是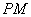 的中点,
的中点,
∴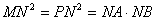 , ∴
, ∴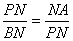 ,
,
又∵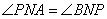 , ∴△
, ∴△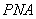 ∽△
∽△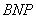 ,
,
∴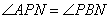 , 即
, 即 .
.
∵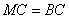 , ∴
, ∴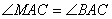 , ∴
, ∴ ,
,
∴△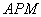 ∽△
∽△ . ………5分
. ………5分
(2)∵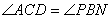 ,∴
,∴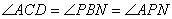 ,即
,即 ,
,
∴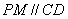 , ∵△
, ∵△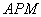 ∽△
∽△ ,∴
,∴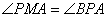 ,
,
∵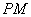 是圆
是圆 的切线,∴
的切线,∴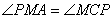 ,
,
∴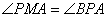
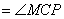 ,即
,即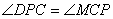 ,
,
∴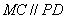 , ∴四边形PMCD是平行四边形. ………10分
, ∴四边形PMCD是平行四边形. ………10分
【思路点拨】(I)由切割线定理,及N是PM的中点,可得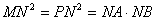 ,进而
,进而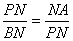 ,结合
,结合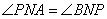 ,可得△
,可得△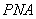 ∽△
∽△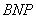 ,则
,则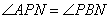 ,即
,即 ;再由MC=BC,可得∠MAC=∠BAC,再由等角的补角相等可得∠MAP=∠PAB,进而得到△APM∽△ABP(II)由∠ACD=∠PBN,可得∠PCD=∠CPM,即PM∥CD;由△APM∽△ABP,PM是圆O的切线,可证得∠MCP=∠DPC,即MC∥PD;再由平行四边形的判定定理得到四边形PMCD是平行四边形.
;再由MC=BC,可得∠MAC=∠BAC,再由等角的补角相等可得∠MAP=∠PAB,进而得到△APM∽△ABP(II)由∠ACD=∠PBN,可得∠PCD=∠CPM,即PM∥CD;由△APM∽△ABP,PM是圆O的切线,可证得∠MCP=∠DPC,即MC∥PD;再由平行四边形的判定定理得到四边形PMCD是平行四边形.


科目:高中数学 来源: 题型:
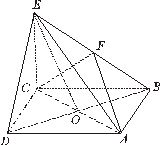
在四棱锥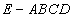 中,底面
中,底面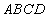 是正方形,
是正方形,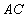 与
与 交于点
交于点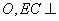 底面
底面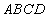 ,
,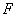 为
为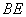 的中点.
的中点.
(1)求证: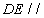 平面
平面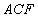 ;
;
(2)若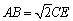 ,在线段
,在线段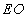 上是否存在点
上是否存在点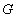 ,使
,使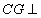 平面
平面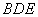 ?若存在,求出
?若存在,求出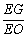 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com