
在四棱锥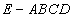 中,底面
中,底面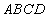 是正方形,
是正方形,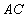 与
与 交于点
交于点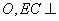 底面
底面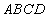 ,
,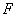 为
为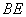 的中点.
的中点.
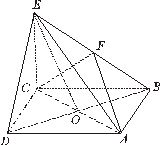
(1)求证: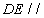 平面
平面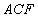 ;
;
(2)若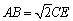 ,在线段
,在线段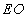 上是否存在点
上是否存在点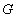 ,使
,使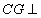 平面
平面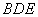 ?若存在,求出
?若存在,求出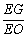 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
如图所示,已知圆 外有一点
外有一点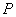 ,作圆
,作圆 的切线
的切线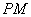 ,
,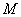 为切点,过
为切点,过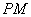 的中点
的中点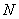 ,作割线
,作割线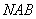 ,交圆于
,交圆于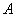 、
、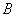 两点,连接
两点,连接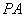 并延长,交圆
并延长,交圆 于点
于点 ,连接
,连接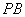 交圆
交圆 于点
于点 ,若
,若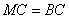 .
.
(1)求证:△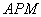 ∽△
∽△ ;
;
(2)求证:四边形 是平行四边形.
是平行四边形.

查看答案和解析>>
科目:高中数学 来源: 题型:
在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:
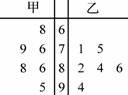
(Ⅰ)若从甲、乙两名学生中选择1人参加该知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(Ⅱ)若从学生甲的6次培训成绩中随机选择2个,记选到的分数超过87分的个数为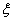 ,求
,求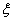 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数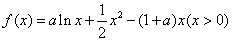 ,其中
,其中 为实数.
为实数.
(1)求函数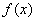 的单调区间;
的单调区间;
(2)若函数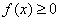 对定义域内的任意
对定义域内的任意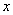 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(3)证明,对于任意的正整数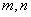 ,不等式
,不等式
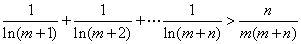 恒成立.
恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com