
已知数列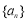 满足
满足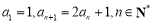 .
.
(1)证明数列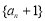 为等比数列,并求出数列
为等比数列,并求出数列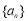 的通项公式;
的通项公式;
(2)若数列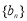 满足
满足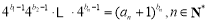 .证明:数列
.证明:数列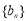 是等差数列.
是等差数列.
(3)证明: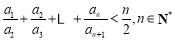 .
.
(1)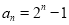 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)证明数列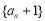 为等比数列,就是证明
为等比数列,就是证明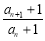 为一个常数. 因为
为一个常数. 因为 ,所以
,所以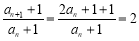 ,所以,
,所以,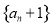 是以2为首项,2为公比的等比数列. 则
是以2为首项,2为公比的等比数列. 则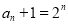 ,即
,即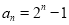 ,
, ;(2)证明数列
;(2)证明数列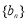 是等差数列,就是要证明
是等差数列,就是要证明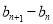 为一个常数.首先化简等式
为一个常数.首先化简等式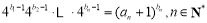 ,即
,即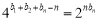 ,所以
,所以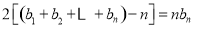 ,这实质是
,这实质是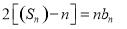 ,因此作差消去
,因此作差消去 得:
得: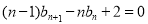 ,再作差消去常数得:
,再作差消去常数得: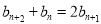 ,
,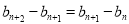 ,即
,即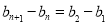 ;(3)证明数列不等式,一般有两个思路,一是求和,二是放缩.本题由于通项
;(3)证明数列不等式,一般有两个思路,一是求和,二是放缩.本题由于通项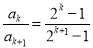 不适宜求和,所以尝试放缩,即利用变量分离进行放缩,由
不适宜求和,所以尝试放缩,即利用变量分离进行放缩,由 ,得
,得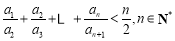 .
.
试题解析:(1)因为 ,所以
,所以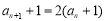 ,且
,且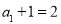 ,
,
所以,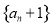 是以2为首项,2为公比的等比数列. 2分
是以2为首项,2为公比的等比数列. 2分
则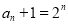 ,即
,即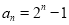 ,
, . 3分
. 3分
(2)因为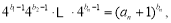 所以.
所以.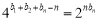 4分
4分
所以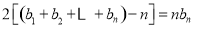 ①
①
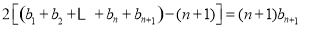 ② 6分
② 6分
②-①,得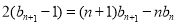
即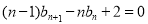 ③
③
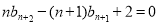 ④ 8分
④ 8分
④-③,得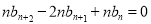 ,
,
即 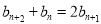
得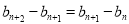 ,
, 10分
10分
所以数列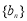 为等差数列.
为等差数列.
(3)因为 ,
,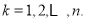 11分
11分
所以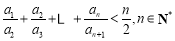 . 12分
. 12分
考点:用定义证明等差数列、等比数列,放缩法证明数列不等式


科目:高中数学 来源:2016届四川绵阳南山中学高一下学期3月月考数学试卷(解析版) 题型:选择题
设M是平行四边形ABCD的对角线的交点,O为任意一点,则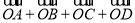 =( )
=( )
A.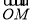 B.
B.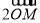
C.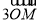 D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届四川省资阳市高一下学期期末考试数学试卷(解析版) 题型:选择题
如图,在5个并排的正方形图案中作出一个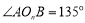 (
(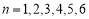 ),则
),则 ( )
( )
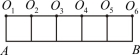
A.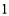 ,
, B.
B.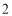 ,
, C.
C.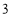 ,
, D.
D. ,
,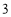 ,
, ,
,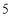
查看答案和解析>>
科目:高中数学 来源:2016届吉林省高一教学评估(一)数学试卷(解析版) 题型:选择题
数列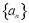 中,a1,a2-a1,a3-a2,,an-an-1是首项为1、公比为
中,a1,a2-a1,a3-a2,,an-an-1是首项为1、公比为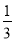 的等比数列,则an等于( )
的等比数列,则an等于( )
(A) (B)
(B)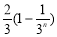 (C)
(C)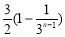 (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com