
 的左、右两个焦点,椭圆C上一点P(1,
的左、右两个焦点,椭圆C上一点P(1, )到F1、F2两点的距离之和等于4.又直线l:y=
)到F1、F2两点的距离之和等于4.又直线l:y= x+m与椭圆C有两个不同的交点A、B,O为坐标原点.
x+m与椭圆C有两个不同的交点A、B,O为坐标原点.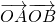 的取值范围.
的取值范围. )在椭圆上,∴
)在椭圆上,∴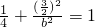 ,解得b2=3.(2分)
,解得b2=3.(2分) . (3分)
. (3分) x+m经过点F1(-1,0),
x+m经过点F1(-1,0), ×(-1)+m,∴m=
×(-1)+m,∴m= . (5分)
. (5分)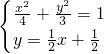 ,消去x,整理得16y2-12y-9=0,
,消去x,整理得16y2-12y-9=0, ,y1y2=-
,y1y2=- . (6分)
. (6分) |F1F2||y2-y1|=
|F1F2||y2-y1|= ×2
×2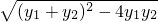 =
=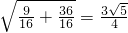
 ,消去y,整理得x2+mx+m2-3=0 ①
,消去y,整理得x2+mx+m2-3=0 ① x1+m)(
x1+m)( x2+m)=
x2+m)= x1x2+
x1x2+ (x1+x2)m+m2
(x1+x2)m+m2 (m2-3)+
(m2-3)+ (-m)m+m2=
(-m)m+m2= m2-
m2- . (10分)
. (10分) =x1x2+y1y2=m2-3+
=x1x2+y1y2=m2-3+ m2-
m2- =
= m2-
m2- ,(11分)
,(11分) ≤
≤
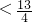 .
. 的取值范围是[-
的取值范围是[- ,
, ). (14分)
). (14分) )在椭圆上,解得b,最后写出椭圆C的标准方程;
)在椭圆上,解得b,最后写出椭圆C的标准方程; x+m经过点F1求得m,设A、B两点的坐标分别为(x1,y1)、(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△ABF2的面积,从而解决问题.
x+m经过点F1求得m,设A、B两点的坐标分别为(x1,y1)、(x2,y2),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得△ABF2的面积,从而解决问题.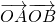 的取值范围.
的取值范围.

 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点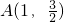 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com