
(本题满分12分)若函数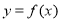 对任意的
对任意的
 ,恒有
,恒有 .当
.当 时,恒有
时,恒有 .
.
(1)判断函数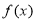 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2)判断函数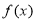 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(3)若 ,解不等式
,解不等式 .
.
(1) 为奇函数,证明详见解析;(2)
为奇函数,证明详见解析;(2) 为
为 上的减函数,证明详见解析;(3)解集为:
上的减函数,证明详见解析;(3)解集为: .
.
【解析】
试题分析:(1)抽象函数奇偶性的判断更要紧扣定义,用好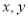 所取的特殊值,及它们之间的特殊关系,如
所取的特殊值,及它们之间的特殊关系,如 取一些特殊值
取一些特殊值 ,
,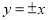 ,
,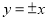 等,问题往往就有所突破;(2)抽象函数单调性的判断也要紧扣定义,用好已知条件中的不等关系;(3)解抽象不等式主要是运用抽象函数本身的单调性,这里是运用(2)得出的结论来解题.
等,问题往往就有所突破;(2)抽象函数单调性的判断也要紧扣定义,用好已知条件中的不等关系;(3)解抽象不等式主要是运用抽象函数本身的单调性,这里是运用(2)得出的结论来解题.
试题解析:(1)令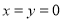 ,可知
,可知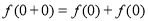 ,解得
,解得
又 ,移项,
,移项,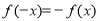 ,所以
,所以 为奇函数;
为奇函数;
(2)设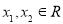 ,且
,且 ,则
,则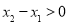 ,由已知条件知
,由已知条件知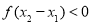 ,从而
,从而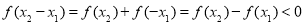 ,即
,即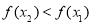 ,对照定义知:
,对照定义知: 为
为 上的减函数;
上的减函数;
(3)由已知条件知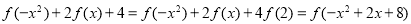 ,又
,又 ,所以原不等式
,所以原不等式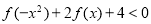 可化为
可化为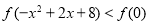 ,又因为
,又因为 为
为 上的减函数,所以
上的减函数,所以 ,解得
,解得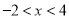 ,即原不等式的解集为:
,即原不等式的解集为: .
.
考点:抽象函数性质的研究及运用.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源:2014-2015学年安徽省高二10月月考文科数学试卷(解析版) 题型:选择题
设命题甲:|x-2|<3,命题乙: ,那么甲是乙的( )
,那么甲是乙的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年宁夏高二上学期第一次月考理科数学试卷(解析版) 题型:选择题
执行下面的程序框图,如果输入的N=4,那么输出的S=()

A.1
B.1+
C.1+ +
+ +
+ +
+
D.1+ +
+ +
+ +
+
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com