
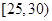 ,第2组
,第2组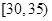 ,第3组
,第3组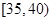 ,第4组
,第4组 ,第5组
,第5组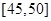 ,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。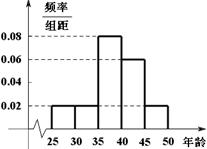
| 区间 | 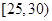 | 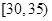 | 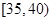 |  | 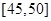 |
| 人数 | 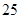 | a | b | | |
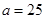 人,
人,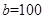 人,
人,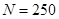 人;(2)第1,2,3组分别抽取1人,1人,4人;
人;(2)第1,2,3组分别抽取1人,1人,4人;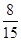
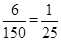 即可解决问题;
即可解决问题;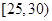 与
与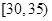 两组的人数相同,
两组的人数相同,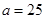 人. 1分
人. 1分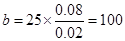 人. 2分
人. 2分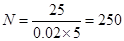 人. 3分
人. 3分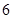 人,每组抽取的人数分别为:
人,每组抽取的人数分别为: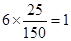 , 4分
, 4分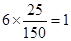 , 5分
, 5分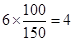 , 6分
, 6分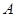 ,第2组的1人为
,第2组的1人为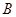 ,第3组的4人分别为
,第3组的4人分别为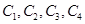 ,则从6人中抽取2人的所有可能结果为:
,则从6人中抽取2人的所有可能结果为: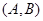 ,
,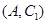 ,
,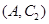 ,
,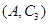 ,
,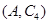 ,
,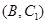 ,
,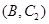 ,
,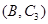 ,
,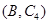 ,
,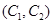 ,
,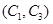 ,
,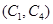 ,
,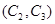 ,
,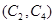 ,
,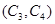 ,
,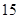 种. 9分
种. 9分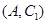 ,
,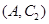 ,
,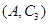 ,
,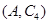 ,
,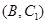 ,
,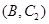 ,
,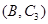 ,
,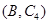 ,
,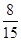 .12分
.12分

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级. 某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为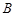 的考生有
的考生有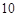 人.
人. 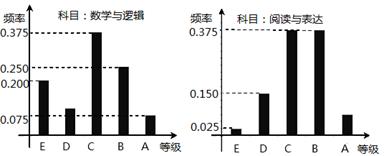
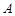 的人数;
的人数; 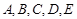 分别对应
分别对应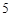 分,
分,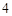 分,
分,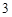 分,
分,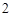 分,
分,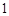 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分; 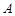 . 在至少一科成绩为
. 在至少一科成绩为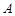 的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为
的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为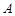 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 60分 以下 | 61~ 70分 | 71~ 80分 | 81~ 90分 | 91~ 100分 |
| 甲班 (人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班 (人数) | 4 | 8 | 13 | 15 | 10 |
| | 优秀人数 | 非优秀人数 | 总计 |
| 甲班 | | | |
| 乙班 | | | |
| 总计 | | | |
 ,
,
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.数据5,4,4,3,5,2的众数是4 |
| B.一组数据的标准差是这组数据的方差的平方 |
| C.数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 |
| D.频率分布直方图中各小长方形的面积等于相应各组的频数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 男 | 女 | 总计 |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.500人 | B.1000人 | C.1500人 | D.2000人 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | y1 | y2 | 总计 |
| x1 | a | 40 | 94 |
| x2 | 32 | 63 | 95 |
| 总计 | 86 | b | 189 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com