
已知圆 经过椭圆
经过椭圆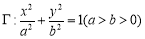 的右焦点
的右焦点 和上顶点
和上顶点 .
.
(1)求椭圆 的方程;
的方程;
(2)过原点 的射线
的射线 与椭圆
与椭圆 在第一象限的交点为
在第一象限的交点为 ,与圆
,与圆 的交点为
的交点为 ,
, 为
为 的中点,求
的中点,求 的最大值.
的最大值.

(1)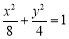 ;(2)
;(2)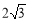 .
.
【解析】
试题分析:本题考查直线、圆、椭圆、平面向量、分式函数等基础知识,考查直线与圆锥曲线的位置关系;考查运算求解能力、推理论证能力;考查数形结合、化归与转化及函数与方程等数学思想.第一问,数形结合,令y=0,x=0即可分别求出c和b的值,从而得到椭圆的标准方程;第二问,设出直线方程和P、Q点坐标,令直线与椭圆联立得到Q点横坐标,利用向量的数量积,将P、Q点坐标代入,得到关于k的表达式,利用导数求函数的最值;法二,将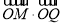 进行转化,变成
进行转化,变成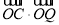 ,再利用配方法求最值.
,再利用配方法求最值.
试题解析:(1)在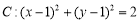 中,
中,
令 得
得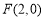 ,即
,即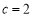 ,令
,令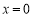 ,得
,得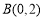 ,即
,即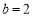 , 2分
, 2分
由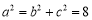 ,∴椭圆
,∴椭圆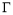 :
: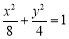 . 4分
. 4分
(2)法一:依题意射线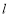 的斜率存在,设
的斜率存在,设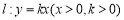 ,设
,设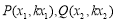 -5分
-5分
 得:
得: ,∴
,∴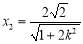 . 6分
. 6分
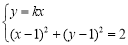 得:
得: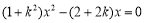 ,∴
,∴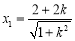 , 7分
, 7分
∴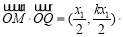
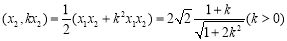 . 9分
. 9分
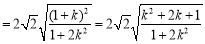 .
.
设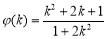 ,
,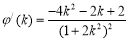 ,
,
令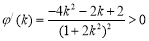 ,得
,得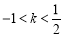 .
.
又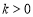 ,∴
,∴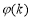 在
在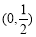 单调递增,在
单调递增,在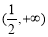 单调递减. 11分
单调递减. 11分
∴当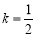 时,
时,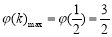 ,即
,即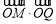 的最大值为
的最大值为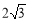 . 13分
. 13分
法二:依题意射线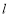 的斜率存在,设
的斜率存在,设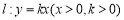 ,设
,设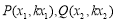 5分
5分
 得:
得: ,∴
,∴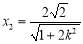 . 6分
. 6分

=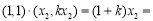
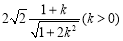 9分
9分
 .
.
设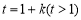 ,则
,则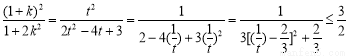 .
.
当且仅当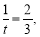 即
即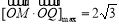 .
.
法三:设点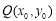 ,
,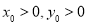 ,
,
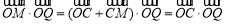 6分
6分
=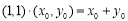 . 7分
. 7分
又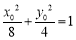 ,
,
设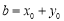 与
与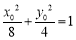 联立得:
联立得: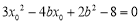 . 9分
. 9分
令 . 11分
. 11分
又点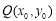 在第一象限,∴当
在第一象限,∴当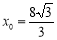 时,
时,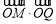 取最大值
取最大值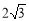 . 13分
. 13分
考点:直线、圆、椭圆、平面向量、分式函数.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,如果输出的结果为 ,则判断框内应填入的条件是( )
,则判断框内应填入的条件是( )
A.k<3 B.k>3 C.k<4 D.k>4

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省漳州市毕业班质量检查理科数学试卷(解析版) 题型:选择题
已知函数 的定义域为[a,b],值域为[-2,1],则
的定义域为[a,b],值域为[-2,1],则 的值不可能是
的值不可能是
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试理科数学试卷(解析版) 题型:选择题
甲、乙、丙、丁四个人排成一行,则乙、丙位于甲的同侧的排法种数是( )
A.16 B.12 C.8 D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试文科数学试卷(解析版) 题型:选择题
下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
A.y= B.y=
B.y=
C.y=-x2+2 D.y=lg|x|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com