设函数f(x)定义域为R,当x>0时,f(x)>1,且对任意x,y∈R,有f(x+y)=f(x)•f(y).
(1)证明:f(0)=1;
(2)证明:f(x)在R上是增函数;
(3)设集合A={(x,y)|f(x2)•f(y2)<f(1)},B={(x,y)|f(x+y+c)=1,c∈R},若A∩B=φ,求c的取值范围.
(1)证明:设x=0,y=1得:f(0+1)=f(0)•f(1),即f(1)=f(0)•f(1)
∵f(1)>1
∴f(0)=1
(2)证明:∵对x
1,x
2∈R,x
1<x
2,,有x
2-x
1>0
∴f(x
2)=f(x
1+x
2-x
1)=f(x
1)•f(x
2-x
1)中有f(x
2-x
1)>1
由已知可,得当x
1>0时,f(x
1)>1>0
当x
1=0时,f(x
1)=1>0
当x
1<0时,f(x
1)•f(-x
1)=f(x
1-x
1)=f(0)=1
又∵f(-x
1)>1∴0<f(x
1)<1
故对于一切x
1∈R,有f(x
1)>0
∴f(x
2)=f(x
1)•f(x
2-x
1)>f(x
1),故命题得证.
(3)解 由f(x
2+y
2)<f(1),则由单调性知x
2+y
2<1.
由f(x+y+c)=f(0)=1和函数单调性知x+y+c=0,
若A∩B=φ,则只要圆x
2+y
2=1与直线x+y+c=0相离或相切即可,故
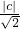
≥1.
∴c≥

或c≤

分析:(1)为使f(x+y)=f(x)•f(y)中有f(0),由当x>0时,f(x)>1.可设x=0,y=1可得f(1)=f(0)•f(1),结合f(1)>1可求f(0)
(2)要证明f(x)在R上是增函数,即证明当x
1<x
2时,有f(x
1)<f(x
2),当x
1,x
2∈R,x
1<x
2,,有x
2-x
1>0,则f(x
2)=f(x
1+x
2-x
1)=f(x
1)•f(x
2-x
1),可证
(3)由f(x
2+y
2)<f(1)及单调性知x
2+y
2<1可求A;由f(x+y+c)=f(0)=1和函数单调性知x+y+c=0可求B,若A∩B=φ,用图形分析可得:只要圆x
2+y
2=1与直线x+y+c=0相离或相切即可
点评:本题主要考查了利用抽象函数的赋值法求解函数值,及利用构造法证明函数的单调性的技巧要求考生熟练应用,利用函数的单调性把集合的基本运算转化为直线与圆的位置关系,本题是一道构思非常巧妙的试题.

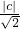 ≥1.
≥1. 或c≤
或c≤


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案