
设各项均为正数的数列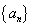 的前
的前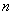 项和为
项和为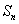 ,满足
,满足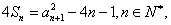 且
且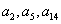 构成等比数列.
构成等比数列.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:
采用系统抽样方法从960人中抽取32人做问卷调查.为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间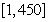 的人做问卷
的人做问卷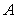 ,编号落入区间
,编号落入区间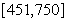 的人做问卷
的人做问卷 ,其余的人做问卷
,其余的人做问卷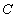 ,则抽到的人中,做问卷
,则抽到的人中,做问卷 的人数为( )
的人数为( )
A.7 B.9 C.10 D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com