
 分)某班有两个课外活动小组,其中第一小组有足球票6张,排球票 4张;第二小组有足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,和乙从第二小组的10张票中任抽1张.
分)某班有两个课外活动小组,其中第一小组有足球票6张,排球票 4张;第二小组有足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,和乙从第二小组的10张票中任抽1张.
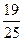
 ,“乙从第二小组的10张票中任抽1张,抽到排球票”为事件
,“乙从第二小组的10张票中任抽1张,抽到排球票”为事件 ,
, ,
, ;
; ,
, .
. 独立事件. 6分
独立事件. 6分 =
= .
. . 9分
. 9分 ·
· 发生)的概率为:
发生)的概率为: ·
· )=P(
)=P( )·P(
)·P( )=
)= =
= .
. ·
· )=1-
)=1- =
=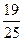 . 11分
. 11分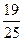 . 12分
. 12分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
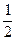 ,乙投篮命中的概率为
,乙投篮命中的概率为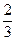 .
. 2个的概率;
2个的概率;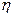 的概率分布和数学期望.
的概率分布和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。
50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。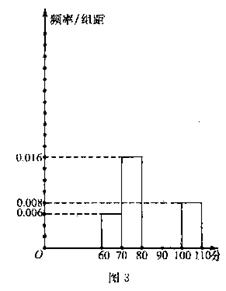
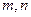 ,求
,求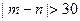 的概率;
的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 过第二
过第二 次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。
次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。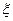 ,求随机变量
,求随机变量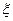 的期望。
的期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
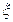 ~
~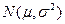 ,且
,且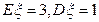 ,那么
,那么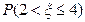 等于( )
等于( )| A.0.5 | B.0.683 | C.0.954 | D.0.997 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com