
分析 (Ⅰ)方程x2+ky2=2可化为$\frac{{y}^{2}}{\frac{2}{k}}+\frac{{x}^{2}}{2}=1$,利用方程x2+ky2=2表示焦点在y轴上的椭圆,建立不等式,即可求实数k的取值范围;
(Ⅱ)设|PF1|=x,|PF2|=y,根据足$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0判断出∠PF1F2=90°进而根据三角形面积公式求得xy,最后根据勾股定理求得x2+y2的值,进而求得y-x,根据双曲线定义求得a,最后根据a和c求得b,双曲线方程可得.
解答 解:(Ⅰ)方程x2+ky2=2可化为$\frac{{y}^{2}}{\frac{2}{k}}+\frac{{x}^{2}}{2}=1$,
∵表示焦点在y轴上的椭圆,
∴$\frac{2}{k}$>2,
∴0<k<1;
(Ⅱ)设|PF1|=x,|PF2|=y,x>y,
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,
∴∠PF1F2=90°,
∴$\frac{1}{2}$xy=1,xy=2,
∵F1F1=2$\sqrt{5}$,
∴x2+y2=20,
∴y-x=$\sqrt{{x}^{2}+{y}^{2}-2xy}$=4,
∵y-x=2a=4,
∴a=2,
∴b=1.
∴双曲线方程为$\frac{{x}^{2}}{4}-{y}^{2}=1$.
点评 本题主要考查了椭圆、双曲线的标准方考查学生的计算能力,属于中档题.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
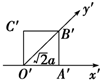
| A. | $\frac{\sqrt{2}}{4}$a2 | B. | a2 | C. | 2$\sqrt{2}$a2 | D. | 2a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x-2 | B. | y=log2x | C. | y=x2+1 | D. | y=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 120° | C. | 135° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com