
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
105 |
已知在全部105人中随机抽取一人为优秀的概率为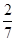 .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,若按97.5%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10或11号的概率.
参考公式和数据: 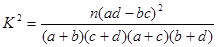
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
(1)
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
10 |
45 |
55 |
|
乙班 |
20 |
30 |
50 |
|
合计 |
30 |
75 |
105 |
(2)有97.5%的把握认为成绩与班级有关系(3)
【解析】
试题分析:(1)列联表为
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
10 |
45 |
55 |
|
乙班 |
20 |
30 |
50 |
|
合计 |
30 |
75 |
105 |
4分
(2)根据列联表的数据,得到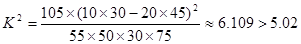 ,
,
因此有97.5%的把握认为成绩与班级有关系. 8分
(3)设“抽到10或11号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为
(x,y),所有基本事件有(1,1)、(1,2)、(1,3)、…(6,6),共36个.
事件A包含的基本事件有(4,6)、(5,5)、(6,4)、(5,6)、(6,5)共5个,
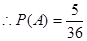 . 12分
. 12分
考点:本小题主要考查列联表的性质,独立性检验的应用和古典概型概率的计算.
点评:根据列联表中的数据求得 后,要注意回答问题的准确性;古典概型概率的计算比较简单,但要注意各个事件必须是等可能的,否则不能用古典概型概率公式求解.
后,要注意回答问题的准确性;古典概型概率的计算比较简单,但要注意各个事件必须是等可能的,否则不能用古典概型概率公式求解.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
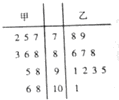 从甲、乙两个班级各随机抽取10名同学的数学成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
从甲、乙两个班级各随机抽取10名同学的数学成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.| 分组 | 频数 | 频率 |
| [70,80) | ||
| [80,90) | ||
| [90,100) | ||
| [100,110) |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省示范高中高三(上)摸底数学试卷(文科)(解析版) 题型:解答题
| 分组 | 频数 | 频率 |
| [70,80) | ||
| [80,90) | ||
| [90,100) | ||
| [100,110) |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com