Question

18．一个三棱锥的6条棱中有5条长是1，余下的棱长是x，则该三棱锥的体积最大值是$\frac{1}{8}$；表面积最大值是1+$\frac{\sqrt{3}}{2}$；x的取值范围是（0，$\sqrt{3}$）．

Answer 1

分析 做出图形，设AC=x，二面角A-BD-C为α，则当α=90°时，棱锥的体积最大，求出S_△ACD关于x的表达式，得出表面积的最大值，在△ACE中使用余弦定理求出x的范围．

解答 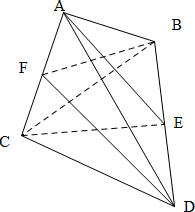解：设三棱锥A-BCD中，AC=x，其余各棱均为1，则△BCD，△ABD为边长为1的正三角形．
设E为BD的中点，F为AC的中点，二面角A-BD-C的大小为α，则∠AEC=α．AE=CE=$\frac{\sqrt{3}}{2}$，
∴V_A-BCD=$\frac{1}{3}$S_△ACE•BD=$\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}sinα×1$=$\frac{sinα}{8}$．
∴当α=90°时，三棱锥的体积取得最大值$\frac{1}{8}$．
∵DF=BF=$\sqrt{1-\frac{{x}^{2}}{4}}$，
∴S_△ABC=S_△ACD=$\frac{1}{2}•x•\sqrt{1-{x}^{2}}$=$\sqrt{\frac{{x}^{2}}{4}（1-\frac{{x}^{2}}{4}）}$≤$\frac{1}{2}$，
∴三棱锥的表面积S=2S_△ACD+2S_△BCD≤2×$\frac{1}{2}$+2×$\frac{\sqrt{3}}{4}$=1+$\frac{\sqrt{3}}{2}$．
在△ACE中，由余弦定理得AC=$\sqrt{A{E}^{2}+C{E}^{2}-2AE•CEcosα}$=$\sqrt{\frac{3}{2}（1-cosα）}$．
∵0＜α＜π，
∴0$＜AC＜\sqrt{3}$．
故答案为：$\frac{1}{8}$，1+$\frac{\sqrt{3}}{2}$，（0，$\sqrt{3}$）．

点评 本题考查了棱锥的结构特征，体积，表面积计算，属于中档题．