
| A. | 买1张肯定不中奖 | B. | 买1000张一定能中奖 | ||
| C. | 买1000张也不一定能中奖 | D. | 买1000张一定恰有1张能中奖 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | lga>lgb | C. | 2a>2b | D. | $\frac{1}{b}$>$\frac{1}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ+μ=2 | B. | λ-μ=1 | C. | λμ=-1 | D. | λμ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
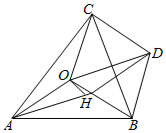 在△ABC中,∠BAC=45°,∠ABC=60°,O为三角形的外心,以线段OB,OC为邻边作平行四边形,第四个顶点为D,再以OA,OD为邻边作平行四边形,它的第四个顶点为H.
在△ABC中,∠BAC=45°,∠ABC=60°,O为三角形的外心,以线段OB,OC为邻边作平行四边形,第四个顶点为D,再以OA,OD为邻边作平行四边形,它的第四个顶点为H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
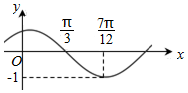 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | ω=2,φ=$\frac{π}{6}$ | B. | ω=2,φ=$\frac{π}{3}$ | C. | ω=1,φ=$\frac{π}{6}$ | D. | ω=1,φ=$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校从高一年级A,B两个班中各选出7名学生参加物理竞赛,他们的成绩(单位:分)的茎叶图如图所示,其中A班学生的平均分是85分
某校从高一年级A,B两个班中各选出7名学生参加物理竞赛,他们的成绩(单位:分)的茎叶图如图所示,其中A班学生的平均分是85分查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
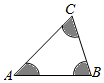 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com