
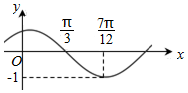
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | ω=2,φ=$\frac{π}{6}$ | B. | ω=2,φ=$\frac{π}{3}$ | C. | ω=1,φ=$\frac{π}{6}$ | D. | ω=1,φ=$\frac{π}{3}$ |
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 买1张肯定不中奖 | B. | 买1000张一定能中奖 | ||
| C. | 买1000张也不一定能中奖 | D. | 买1000张一定恰有1张能中奖 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
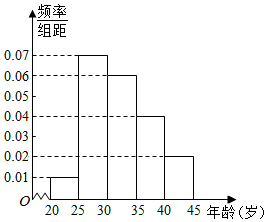 为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人
为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网络纸上正方形的边长为l,粗线画出的是某几何体的三视图,则该几何体的外接球表面积为( )
如图,网络纸上正方形的边长为l,粗线画出的是某几何体的三视图,则该几何体的外接球表面积为( )| A. | 12π | B. | 34π | C. | $\frac{17π}{4}$ | D. | 17π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点
如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com