
分析 (1)直接化简f(α)=cosα,由α为第二象限角求出sinα,再由二倍角公式化简计算得答案;
(2)由5f(α)=4f(3α+2β),得5cos[(2α+β)-(α+β)]=4cos[(2α+β)+(α+β)],进一步化简可得cos(2α+β)cos(α+β)=-9sin(2α+β)sin(α+β),由已知条件可得cos(2α+β)cos(α+β)≠0,即可求出答案.
解答 解:f(α)=$\frac{cos(π-α)sin(\frac{3}{2}π+α)}{cosα}$=$\frac{(-cosα)(-cosα)}{cosα}=cosα$,
(1)$f(α)=cosα=-\frac{3}{5}$,α为第二象限角,得$sinα=\frac{4}{5}$.
$\frac{sin2α+cos2α+1}{1+tanα}$=$\frac{2sinαcosα+co{s}^{2}α-si{n}^{2}α+1}{1+\frac{sinα}{cosα}}$
=$\frac{{2×\frac{4}{5}×(-\frac{3}{5})+\frac{9}{25}-\frac{16}{25}+1}}{{1+(-\frac{4}{3})}}=\frac{18}{25}$;
(2)∵5f(α)=4f(3α+2β),
∴5cos[(2α+β)-(α+β)]=4cos[(2α+β)+(α+β)].
可得:5[cos(2α+β)cos(α+β)+sin(2α+β)sin(α+β)]
=4[cos(2α+β)cos(α+β)-sin(2α+β)sin(α+β)],
化简:cos(2α+β)cos(α+β)=-9sin(2α+β)sin(α+β).
又$α+β≠kπ+\frac{π}{2},\;\;2α+β≠kπ+\frac{π}{2}\;,k∈Z$
知cos(2α+β)cos(α+β)≠0
故tan(2α+β)•tan(α+β)=$-\frac{1}{9}$.
综上tan(2α+β)•tan(α+β)是定值$-\frac{1}{9}$.
点评 本题考查三角函数化简求值,考查同角三角函数的基本关系式的应用,考查计算能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
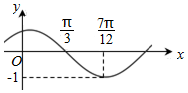 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | ω=2,φ=$\frac{π}{6}$ | B. | ω=2,φ=$\frac{π}{3}$ | C. | ω=1,φ=$\frac{π}{6}$ | D. | ω=1,φ=$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
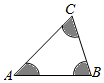 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-7=0 | B. | x+2y-5=0 | C. | x-2y-1=0 | D. | 2x-y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
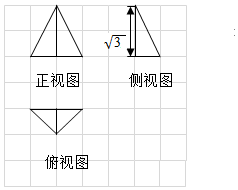 网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )
网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com