
【题目】已知函数f(x)= ![]() ,
,
(1)若a=﹣1,求f(x)的单调区间;
(2)若f(x)有最大值3,求a的值.
(3)若f(x)的值域是(0,+∞),求a的取值范围.
【答案】
(1)解:当a=﹣1时,f(x)= ![]() ,
,
令g(x)=﹣x2﹣4x+3,
由于g(x)在(﹣∞,﹣2)上单调递增,在(﹣2,+∞)上单调递减,
而y= ![]() t在R上单调递减,
t在R上单调递减,
所以f(x)在(﹣∞,﹣2)上单调递减,在(﹣2,+∞)上 单调递增,
即函数f( x)的递增区间是(﹣2,+∞),递减区间是(﹣∞,﹣2 ).
(2)解:令h(x)=ax2﹣4x+3,y= ![]() h(x),由于f(x)有最大值3,
h(x),由于f(x)有最大值3,
所以 h(x)应有最小值﹣1,
因此 ![]() =﹣1,
=﹣1,
解得a=1.
即当f(x)有最大值3时,a的值等于1.
(3)解:由指数函数的性质知,
要使y=h(x)的值域为(0,+∞).
应使h(x)=ax2﹣4x+3的值域为R,
因此只能有a=0.
因为若a≠0,则h(x)为二次函数,其值域不可能为R.
故 a的取值范围是{0}.
【解析】(1)当a=1时,f(x)= ![]() ,根据复合函数的单调性(同增异减)即可判断出f(x)的单调区间,(2)令h(x)=ax2﹣4x+3,y=
,根据复合函数的单调性(同增异减)即可判断出f(x)的单调区间,(2)令h(x)=ax2﹣4x+3,y=![]() ,当f(x)有最大值3,则h(x)应有最小值﹣1,代入即可解得a=1,(3)根据指数函数的性质,若y=h(x)的值域为(0,+∞),则h(x)=ax2﹣4x+3的值域为R,分析讨论即可得出a的取值范围是{0}.
,当f(x)有最大值3,则h(x)应有最小值﹣1,代入即可解得a=1,(3)根据指数函数的性质,若y=h(x)的值域为(0,+∞),则h(x)=ax2﹣4x+3的值域为R,分析讨论即可得出a的取值范围是{0}.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C= ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】游乐场推出了一项趣味活动,参加活动者需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数,设两次记录的数分别为x,y,奖励规则如下:
①若xy≤3,则奖励玩具一个;②若xy≥8,则奖励水杯一个;③其余情况奖励饮料一瓶,假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.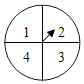
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,Sn=2n﹣an(n∈N*).
(1)计算a2 , a3 , a4 , 并由此猜想通项公式an;
(2)用数学归纳法证明(1)中的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在[﹣1,1]上的奇函数,f(﹣1)=﹣1,且对任意a,b∈[﹣1,1],当a≠b时,都有 ![]() ;
;
(1)解不等式f ![]() ;
;
(2)若f(x)≤m2﹣2km+1对所有x∈[﹣1,1],k∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+(b﹣1)x+3.
(1)若不等式f(x)>0的解为(﹣1, ![]() ),求不等式bx2﹣3x+a≤0的解集;
),求不等式bx2﹣3x+a≤0的解集;
(2)若f(1)=4,a>0,b>0,求ab的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm). 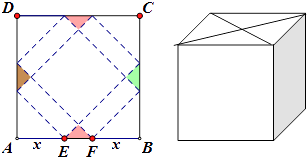
(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD , AD∥BC , AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD , N为PC的中点.
(1)证明MN∥平面PAB;
(2)求四面体N-BCM的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com