
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD , AD∥BC , AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD , N为PC的中点.
(1)证明MN∥平面PAB;
(2)求四面体N-BCM的体积.
【答案】
(1)证明:由已知得AM= ![]() AD=2,如图,
AD=2,如图,
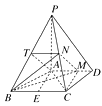
取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN= ![]() BC=2.又AD∥BC,故
BC=2.又AD∥BC,故 ![]() ,所以四边形AMNT为平行四边形,
,所以四边形AMNT为平行四边形,
于是MN∥AT.因为AT平面PAB,MN平面PAB,所以MN∥平面PAB
(2)解:因为PA⊥平面ABCD,N为PC的中点,所以N到平面ABCD的距离为 ![]() PA.
PA.
如图,取BC的中点E,连接AE,由AB=AC=3得AE⊥BC,AE= ![]() =
= ![]() .
.
由AM∥BC得M到BC的距离为 ![]() ,故S△BCM=
,故S△BCM= ![]() ×4×
×4× ![]() =2
=2 ![]() ,
,
所以四面体N-BCM的体积VN-BCM= ![]() ×S△BCM×
×S△BCM× ![]() =
= ![]() .
.
【解析】1.本题考察直线与平面平行的判定及直线与平面平行的性质,由线线平行证线面平行。2.求四面体N-BCM的体积=底面积![]() 高,要想到“PA⊥平面ABCD”的作用,结合题目的已知即可解出。
高,要想到“PA⊥平面ABCD”的作用,结合题目的已知即可解出。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,
,
(1)若a=﹣1,求f(x)的单调区间;
(2)若f(x)有最大值3,求a的值.
(3)若f(x)的值域是(0,+∞),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过焦点垂直长轴的弦长为3.
,过焦点垂直长轴的弦长为3.
(1)求椭圆的标准方程;
(2)过椭圆的右顶点作直线交抛物线y2=2x于A、B两点,求证:OA⊥OB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设(x1 , y1),(x2 , y2),…,(xn , yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( ) 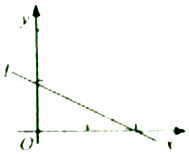
A.x和y的相关系数在﹣1和0之间
B.x和y的相关系数为直线l的斜率
C.当n为偶数时,分布在l两侧的样本点的个数一定相同
D.所有样本点(xi , yi)(i=1,2,…,n)都在直线l上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.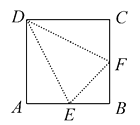
问:
(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点F1(﹣2,0),F2(2,0),且|F1F2|是|PF1|与|PF2|的等差中项,则动点P的轨迹方程是( )
A.![]() +
+ ![]() =1
=1
B.![]() +
+ ![]() =1
=1
C.![]() +
+ ![]() =1
=1
D.![]() +
+ ![]() =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com