
【题目】已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过焦点垂直长轴的弦长为3.
,过焦点垂直长轴的弦长为3.
(1)求椭圆的标准方程;
(2)过椭圆的右顶点作直线交抛物线y2=2x于A、B两点,求证:OA⊥OB.
【答案】
(1)解:椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过焦点垂直长轴的弦长为3,
,过焦点垂直长轴的弦长为3,
则有 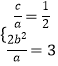 ,
,
解可得a=2,c=1,则b2=a2﹣c2=3.
所以,所求椭圆的标准方程为 ![]()
(2)解:证明:设过椭圆的右顶点(2,0)的直线AB的方程为x=my+2.
代入抛物线方程y2=2x,得y2﹣2my﹣4=0.
设A(x1,y1)、B(x2,y2),
则 ![]() ,
,
∴x1x2+y1y2=(my1+2)(my2+2)+y1y2=(1+m2)y1y2+2m(y1+y2)+4=0.
∴OA⊥OB
【解析】(1)根据题意,分析可得 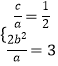 ,解可得a、c的值,由椭圆的定义可得b的值,将a、b的值代入椭圆方程即可得答案;(2)设过椭圆的右顶点(2,0)的直线AB的方程为x=my+2,与抛物线方程联立,设出A、B点的坐标,由根与系数的关系的关系分析计算x1x2+y1y2的值,由向量数量积的性质可得证明.
,解可得a、c的值,由椭圆的定义可得b的值,将a、b的值代入椭圆方程即可得答案;(2)设过椭圆的右顶点(2,0)的直线AB的方程为x=my+2,与抛物线方程联立,设出A、B点的坐标,由根与系数的关系的关系分析计算x1x2+y1y2的值,由向量数量积的性质可得证明.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】游乐场推出了一项趣味活动,参加活动者需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数,设两次记录的数分别为x,y,奖励规则如下:
①若xy≤3,则奖励玩具一个;②若xy≥8,则奖励水杯一个;③其余情况奖励饮料一瓶,假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.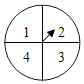
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm). 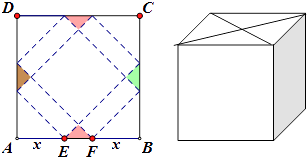
(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,M、N分别是棱SC、BC的中点,且MN⊥AM,若AB=2 ![]() ,则此正三棱锥外接球的体积是( )
,则此正三棱锥外接球的体积是( )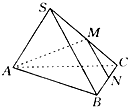
A.12π
B.4 ![]() π
π
C.![]() π
π
D.12 ![]() π
π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A、B、C是三角形的三内角,a、b、c是三内角对应的三边,已知b2 , a2 , c2成等差数列.
(1)求cosA的最小值;
(2)若a=2,当A最大时,△ABC面积的最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(3,+∞)
D.(﹣∞,﹣3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD , AD∥BC , AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD , N为PC的中点.
(1)证明MN∥平面PAB;
(2)求四面体N-BCM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE= ![]() ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2. 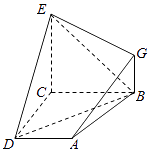
(1)证明:AG∥平面BDE.
(2)求平面BDE和平面ADE所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了四个类比推理: ①由“若a,b,c∈R则(ab)c=a(bc)”类比推出“若a,b,c为三个向量则( ![]()
![]() )
) ![]() =
= ![]() (
( ![]()
![]() )”;
)”;
②“a,b为实数,若a2+b2=0则a=b=0”类比推出“z1 , z2为复数,若 ![]() ”;
”;
③“在平面内,三角形的两边之和大于第三边”类比推出“在空间中,四面体的任意三个面的面积之和大于第四个面的面积”;
④“在平面内,过不在同一条直线上的三个点有且只有一个圆”类比推出“在空间中,过不在同一个平面上的四个点有且只有一个球”.
上述四个推理中,结论正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com