
【题目】如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE= ![]() ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2. 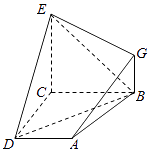
(1)证明:AG∥平面BDE.
(2)求平面BDE和平面ADE所成锐二面角的余弦值.
【答案】
(1)证明:∵平面ABCD⊥平面BCEG,平面ABCD∩平面BCEG=BC
CE⊥BC,CE平面BCEG,
∴EC⊥平面ABCD,
以C为原点,CD为x轴,CB为y轴,CE为z轴,建立空间直角坐标系,
B(0,2,0),D(2,0,0),E(0,0,2),A(2,1,0),G(0,2,1),
设平面BDE的法向量为 ![]() =(x,y,z),
=(x,y,z),
![]() =(0,2,﹣2),
=(0,2,﹣2), ![]() =(2,0,﹣2),
=(2,0,﹣2),
∴ 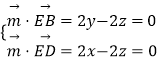 ,取x=1,得
,取x=1,得 ![]() =(1,1,1),
=(1,1,1),
∵ ![]() =(﹣2,1,1),∴
=(﹣2,1,1),∴ ![]() =0,∴
=0,∴ ![]() ⊥
⊥ ![]() ,
,
∵AG平面BDE,∴AG∥平面BDE

(2)解:设平面ADE的法向量 ![]() =(a,b,c),
=(a,b,c),
![]() =(0,1,0),
=(0,1,0), ![]() =(﹣2,0,2),
=(﹣2,0,2),
则 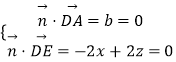 ,取x=1,得
,取x=1,得 ![]() =(1,0,1),
=(1,0,1),
由(1)得平面BDE的法向量为 ![]() =(1,1,1),
=(1,1,1),
设平面BDE和平面ADE所成锐二面角的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴平面BDE和平面ADE所成锐二面角的余弦值为 ![]() .
.
【解析】(1)以C为原点,CD为x轴,CB为y轴,CE为z轴,建立空间直角坐标系,利用向量法能证明AG∥平面BDE.(2)求出平面ADE的法向量和平面BDE的法向量,利用向量法能求出平面BDE和平面ADE所成锐二面角的余弦值.
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)满足 ![]() f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数: ①f(x)=sin
f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数: ①f(x)=sin ![]() x,g(x)=cos
x,g(x)=cos ![]() x;
x;
②f(x)=x+1,g(x)=x﹣1;
③f(x)=x,g(x)=x2 ,
其中为区间[﹣1,1]上的正交函数的组数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过焦点垂直长轴的弦长为3.
,过焦点垂直长轴的弦长为3.
(1)求椭圆的标准方程;
(2)过椭圆的右顶点作直线交抛物线y2=2x于A、B两点,求证:OA⊥OB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设(x1 , y1),(x2 , y2),…,(xn , yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( ) 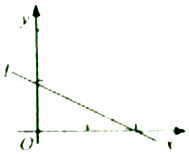
A.x和y的相关系数在﹣1和0之间
B.x和y的相关系数为直线l的斜率
C.当n为偶数时,分布在l两侧的样本点的个数一定相同
D.所有样本点(xi , yi)(i=1,2,…,n)都在直线l上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.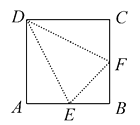
问:
(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且在(0,+∞)上是增函数,设a=f(﹣ ![]() ),b=f(log3
),b=f(log3 ![]() ),c=f(
),c=f( ![]() ),则a、b、c的大小关系是( )
),则a、b、c的大小关系是( )
A.a<c<b
B.b<a<c
C.b<c<a
D.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“可等域函数”,区间A为函数f(x)的一个“可等域区间”.给出下列四个函数: ①f(x)=sin ![]() x;②f(x)=2x2﹣1;③f(x)=|1﹣2x|
x;②f(x)=2x2﹣1;③f(x)=|1﹣2x|
其中存在“可等域区间”的“可等域函数”为( )
A.①
B.②
C.①②
D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com