
【题目】已知f(x)是定义在R上的偶函数,且在(0,+∞)上是增函数,设a=f(﹣ ![]() ),b=f(log3
),b=f(log3 ![]() ),c=f(
),c=f( ![]() ),则a、b、c的大小关系是( )
),则a、b、c的大小关系是( )
A.a<c<b
B.b<a<c
C.b<c<a
D.c<b<a
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,M、N分别是棱SC、BC的中点,且MN⊥AM,若AB=2 ![]() ,则此正三棱锥外接球的体积是( )
,则此正三棱锥外接球的体积是( )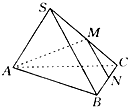
A.12π
B.4 ![]() π
π
C.![]() π
π
D.12 ![]() π
π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE= ![]() ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2. 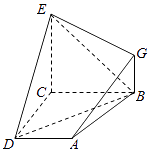
(1)证明:AG∥平面BDE.
(2)求平面BDE和平面ADE所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D﹣AE﹣C为60°,AP=1,AD= ![]() ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.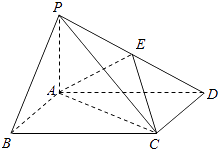
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了考查某厂2000名工人的生产技能情况,随机抽查了该厂n名工人某天的产量(单位:件),整理后得到如下的频率分布直方图(产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35]),其中产量在[20,25)的工人有6名.
(Ⅰ)求这一天产量不小于25的工人人数;
(Ⅱ)工厂规定从产量低于20件的工人中随机的选取2名工人进行培训,求这2名工人不在同一组的概率.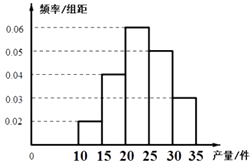
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为 ![]() (a为常数,n∈N*).
(a为常数,n∈N*).
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数a的值及an .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了四个类比推理: ①由“若a,b,c∈R则(ab)c=a(bc)”类比推出“若a,b,c为三个向量则( ![]()
![]() )
) ![]() =
= ![]() (
( ![]()
![]() )”;
)”;
②“a,b为实数,若a2+b2=0则a=b=0”类比推出“z1 , z2为复数,若 ![]() ”;
”;
③“在平面内,三角形的两边之和大于第三边”类比推出“在空间中,四面体的任意三个面的面积之和大于第四个面的面积”;
④“在平面内,过不在同一条直线上的三个点有且只有一个圆”类比推出“在空间中,过不在同一个平面上的四个点有且只有一个球”.
上述四个推理中,结论正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2 ![]() .
.
(1)求cosB;
(2)若a+c=6,△ABC的面积为2,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<a<1,函数f(x)=logax.
(1)若f(5a﹣1)≥f(2a),求实数a的最大值;
(2)当a= ![]() 时,设g(x)=f(x)﹣3x+2m,若函数g(x)在(1,2)上有零点,求实数m的取值范围.
时,设g(x)=f(x)﹣3x+2m,若函数g(x)在(1,2)上有零点,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com