
����Ŀ��Ϊ�˿���ij��2000�����˵���������������������˸ó�n������ij��IJ�������λ��������������õ����µ�Ƶ�ʷֲ�ֱ��ͼ����Ʒ�����ķ�������Ϊ[10��15����[15��20����[20��25����[25��30����[30��35]�������в�����[20��25���Ĺ�����6����
��������һ�������С��25�Ĺ���������
�������涨�Ӳ�������20���Ĺ����������ѡȡ2�����˽�����ѵ������2�����˲���ͬһ��ĸ��ʣ�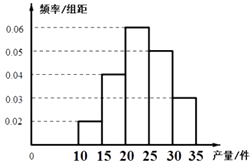
���𰸡��⣺����������ã�����Ϊ[20��25���ĸ���Ϊ0.06��5=0.3
��n= ![]() =20��
=20��
����һ�������С��25�Ĺ�������20��
����һ�������С��25�Ĺ�������Ϊ��0.05+0.03����5��20=8
����������ã�����Ϊ[10��15����������Ϊ20��0.02��5=2��
�����Ƿֱ���A��B��������[15��20����������Ϊ20��0.04��5=4��
�����Ƿֱ�Ϊ�ǣ�a��b��c��d��
��Ӳ�������20���Ĺ�����ѡȡ2�����˵Ľ��Ϊ����A��B������A��a������A��b������A��c����A��d����
��B��a������B��b������B��c����B��d������a��b������a��c������a��d������b��c������b��d������c��d������15�ֽ����
����2�����˲���ͬһ��Ľ��Ϊ
��A��a������A��b������A��c����A��d������B��a������B��b������B��c����B��d������8�֣�
����2�����˲���ͬһ��ĸ���Ϊ�� ![]()
����������1������Ƶ��ֱ��ͼ�ó�����Ϊ[20��25���ĸ���Ϊ0.06��5=0.3�����ݸ��ʿɵõ�����ȡ��20�����˽��е��飬�����õ���һ�������С��25�Ĺ�������8����2������Ƶ��ֱ��ͼ�ɵó�����Ϊ[10��15����������Ϊ2����[15��20����������,4��ʹ���оٷ��õ��Ӳ�������20���Ĺ�����ѡȡ2�����˹���15�ֽ��������2�����˲���ͬһ��Ĺ���8�ֽ�����ʿ����2�����˲���ͬһ��ĸ���.
�����㾫����������Ĺؼ���������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������M����1��0����б��Ϊk��ֱ����Բx2+4x+y2��5=0�ڵ�һ�����ڵIJ����н��㣬��k��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ2a��������ABCD�У�E��F�ֱ�ΪAB��BC���е㣬��ͼ�����߽�3������������ʹ��A��B��C�غϣ��غϺ��Ϊ��P.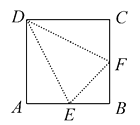
�ʣ�
��1��������γɵļ�������ʲô�����壿
��2����������干�м����棬ÿ������������к��ص㣿
��3��ÿ��������������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}���� ![]()
��1������a1 �� a2 �� a3 �� a4
��2������an�ı���ʽ��������ѧ���ɷ�֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() =1��a��b��0�����ҽ���ΪF2��1��0������P��1��
=1��a��b��0�����ҽ���ΪF2��1��0������P��1�� ![]() ������ԲC�ϣ�
������ԲC�ϣ�
��������ԲC�ķ��̣�
��������ԭ��O������ֱ��EF��MN�ֱ�����ԲC����E��F��M��N�ĵ㣬��ֱ��OE��OM��б��֮��Ϊ�� ![]() ����֤���ı���EMFN�����Ϊ��ֵ��
����֤���ı���EMFN�����Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ƕ�����R�ϵ�ż���������ڣ�0��+�ޣ���������������a=f���� ![]() ����b=f��log3
����b=f��log3 ![]() ����c=f��
����c=f�� ![]() ������a��b��c�Ĵ�С��ϵ�ǣ� ��
������a��b��c�Ĵ�С��ϵ�ǣ� ��
A.a��c��b
B.b��a��c
C.b��c��a
D.c��b��a
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() x3��
x3�� ![]() x2+bx+c������y=f��x���ڵ㣨0��f��0�����������߷���Ϊy=1��
x2+bx+c������y=f��x���ڵ㣨0��f��0�����������߷���Ϊy=1��
��1����b��c��ֵ��
��2����a��0������f��x���ĵ������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����F1����2��0����F2��2��0������|F1F2|��|PF1|��|PF2|�ĵȲ������P�Ĺ켣�����ǣ� ��
A.![]() +
+ ![]() =1
=1
B.![]() +
+ ![]() =1
=1
C.![]() +
+ ![]() =1
=1
D.![]() +
+ ![]() =1
=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2x2+��2��m��x��m��g��x��=x2��x+2m��
��1����m=1����ʽf��x����0�Ľ⼯��
��2����m��0�������x�IJ���ʽf��x����g��x���Ľ⼯��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com