
【题目】若过定点M(﹣1,0)且斜率为k的直线与圆x2+4x+y2﹣5=0在第一象限内的部分有交点,则k的取值范围是 .
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+(b﹣1)x+3.
(1)若不等式f(x)>0的解为(﹣1, ![]() ),求不等式bx2﹣3x+a≤0的解集;
),求不等式bx2﹣3x+a≤0的解集;
(2)若f(1)=4,a>0,b>0,求ab的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm). 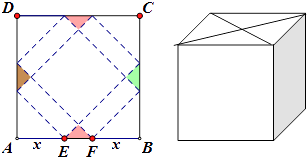
(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1+lnx﹣ ![]() ,其中k为常数.
,其中k为常数.
(1)若k=0,求曲线y=f(x)在点(1,f(1))处的切线方程.
(2)若k=5,求证:f(x)有且仅有两个零点;
(3)若k为整数,且当x>2时,f(x)>0恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,M、N分别是棱SC、BC的中点,且MN⊥AM,若AB=2 ![]() ,则此正三棱锥外接球的体积是( )
,则此正三棱锥外接球的体积是( )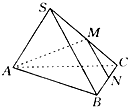
A.12π
B.4 ![]() π
π
C.![]() π
π
D.12 ![]() π
π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A、B、C是三角形的三内角,a、b、c是三内角对应的三边,已知b2 , a2 , c2成等差数列.
(1)求cosA的最小值;
(2)若a=2,当A最大时,△ABC面积的最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD , AD∥BC , AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD , N为PC的中点.
(1)证明MN∥平面PAB;
(2)求四面体N-BCM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了考查某厂2000名工人的生产技能情况,随机抽查了该厂n名工人某天的产量(单位:件),整理后得到如下的频率分布直方图(产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35]),其中产量在[20,25)的工人有6名.
(Ⅰ)求这一天产量不小于25的工人人数;
(Ⅱ)工厂规定从产量低于20件的工人中随机的选取2名工人进行培训,求这2名工人不在同一组的概率.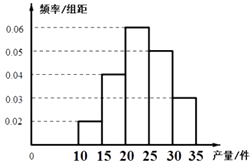
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com