
【题目】数列{an}满足 ![]()
(1)计算a1 , a2 , a3 , a4
(2)猜想an的表达式,并用数学归纳法证明你的结论.
【答案】
(1)解:当n=1时,a1=S1=1.
当n=2时,a1+a2=S2=2×2﹣a2,∴a2= ![]() .
.
当n=3时,a1+a2+a3=S3=2×3﹣a3,∴a3= ![]() .
.
当n=4时,a1+a2+a3+a4=S4=2×4﹣a4,∴a4= ![]() ,
,
由此猜想an= ![]() (n∈N*)
(n∈N*)
(2)解:证明:①当n=1时,a1=S1=1,结论成立.
②假设n=k(k≥1且k∈N*)时,结论成立,即ak= ![]()
那么n=k+1(k≥1且k∈N*)时,ak+1=Sk+1﹣Sk=2(k+1)﹣ak+1﹣2k+ak=2+ak﹣ak+1.
∴2ak+1=2+ak=2+ ![]() =
= ![]() .
.
∴ak+1= ![]() ,
,
由①②可知,对n∈N*,an= ![]() 都成立
都成立
【解析】(1)根据Sn=2n﹣an , 利用递推公式,求出a2 , a3 , a4 . (2)总结出规律求出an , 然后利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
【考点精析】掌握数列的定义和表示和归纳推理是解答本题的根本,需要知道数列中的每个数都叫这个数列的项.记作an,在数列第一个位置的项叫第1项(或首项),在第二个位置的叫第2项,……,序号为n的项叫第n项(也叫通项)记作an;根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
【题目】请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm). 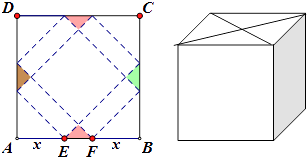
(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD , AD∥BC , AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD , N为PC的中点.
(1)证明MN∥平面PAB;
(2)求四面体N-BCM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE= ![]() ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2. 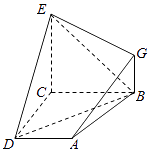
(1)证明:AG∥平面BDE.
(2)求平面BDE和平面ADE所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=a﹣x2( ![]() ≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
A.[1, ![]() +2]
+2]
B.[1,e2﹣2]
C.[ ![]() +2,e2﹣2]
+2,e2﹣2]
D.[e2﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D﹣AE﹣C为60°,AP=1,AD= ![]() ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.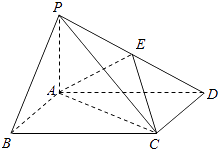
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了考查某厂2000名工人的生产技能情况,随机抽查了该厂n名工人某天的产量(单位:件),整理后得到如下的频率分布直方图(产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35]),其中产量在[20,25)的工人有6名.
(Ⅰ)求这一天产量不小于25的工人人数;
(Ⅱ)工厂规定从产量低于20件的工人中随机的选取2名工人进行培训,求这2名工人不在同一组的概率.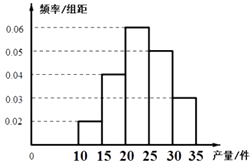
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了四个类比推理: ①由“若a,b,c∈R则(ab)c=a(bc)”类比推出“若a,b,c为三个向量则( ![]()
![]() )
) ![]() =
= ![]() (
( ![]()
![]() )”;
)”;
②“a,b为实数,若a2+b2=0则a=b=0”类比推出“z1 , z2为复数,若 ![]() ”;
”;
③“在平面内,三角形的两边之和大于第三边”类比推出“在空间中,四面体的任意三个面的面积之和大于第四个面的面积”;
④“在平面内,过不在同一条直线上的三个点有且只有一个圆”类比推出“在空间中,过不在同一个平面上的四个点有且只有一个球”.
上述四个推理中,结论正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com