
| A. | (-4,0) | B. | (-∞,-4)∪(0,+∞) | C. | [0,+∞) | D. | (-4,0] |
分析 由题意,检验a=0是否满足条件,当a≠0 时,需满足$\left\{\begin{array}{l}{a>0}\\{△={a}^{2}-4a(a+3)<0}\end{array}\right.$,从而解出实数a的取值范围.
解答 解:因为ax2+ax+a+3>0对一切实数x恒成立,
所以当a=0时,不等式为3>0,满足题意;
当a≠0,需满足$\left\{\begin{array}{l}{a>0}\\{△={a}^{2}-4a(a+3)<0}\end{array}\right.$,解得a>0
总之a≥0
故a的取值范围为:[0,+∞).
故选:C.
点评 本题考查一元二次不等式的应用,注意联系对应的二次函数的图象特征,体现了等价转化和分类讨论的数学思想.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂随机抽取部分工人调查其上班路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),若上班路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某工厂随机抽取部分工人调查其上班路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),若上班路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
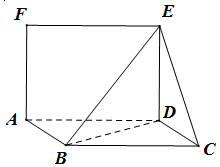 在平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,矩形ADEF中DE=1,且面ADEF⊥面ABCD.
在平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,矩形ADEF中DE=1,且面ADEF⊥面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2${\;}^{\frac{5}{6}}$ | B. | 2${\;}^{\frac{3}{2}}$ | C. | 2${\;}^{\frac{1}{6}}$ | D. | 2${\;}^{(\frac{1}{2})^{\frac{1}{3}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,A是函数f(x)=2x的图象上的动点,过点A作直线平行于x轴,交函数g(x)=2x+2的图象于点B,若函数f(x)=2x的图象上存在点C使得△ABC为等边三角形,则称A为函数f(x)=2x上的好位置点.函数f(x)=2x上的好位置点的个数为( )
如图所示,A是函数f(x)=2x的图象上的动点,过点A作直线平行于x轴,交函数g(x)=2x+2的图象于点B,若函数f(x)=2x的图象上存在点C使得△ABC为等边三角形,则称A为函数f(x)=2x上的好位置点.函数f(x)=2x上的好位置点的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 大于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},+∞)$ | B. | $[\frac{1}{2},+∞)$ | C. | $(\frac{1}{4},+∞)$ | D. | $[\frac{1}{4},+∞)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com