练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝|x2＋2x－1|，若a＜b＜－1，且f(a)＝f(b)，则ab＋a＋b的取值范围是________．

     

    (－1,1)

    【解析】作出函数图象可知若a＜b＜－1，且f(a)＝f(b)，即为a2＋2a－1＝－(b2＋2b－1)，

    整理得(a＋1)2＋(b＋1)2＝4，设θ∈∪，所以ab＋a＋b＝－1＋2sin 2θ∈(－1,1)．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷3练习卷（解析版） 题型：选择题

    在等差数列{an}中，首项a1＝120，公差d＝－4，若Sn≤an(n≥2)，则n的最小值为(　　)

    A．60 B．62 C．70 D．72

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷1练习卷（解析版） 题型：选择题

    若a，b∈R，且ab＞0，则下列不等式中，恒成立的是(　　)

    A．a＋b≥2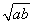 B.＞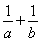

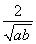
    C.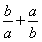≥2 D．a2＋b2＞2ab

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练解答题押题练B组练习卷（解析版） 题型：解答题

    已知函数f(x)＝－x3＋x2，g(x)＝aln x，a∈R.

    (1)若对任意x∈[1，e]，都有g(x)≥－x2＋(a＋2)x恒成立，求a的取值范围；

    (2)设F(x)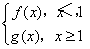＝若P是曲线y＝F(x)上异于原点O的任意一点，在曲线y＝F(x)上总存在另一点Q，使得△POQ中的∠POQ为钝角，且PQ的中点在y轴上，求a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练解答题押题练A组练习卷（解析版） 题型：解答题

    如图，已知椭圆C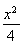：＋y2＝1，A、B是四条直线x＝±2，y＝±1所围成的两个顶点．

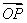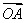    (1)设P是椭圆C上任意一点，若＝m＋n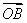，求证：动点Q(m，n)在定圆上运动，并求出定圆的方程；

    (2)若M、N是椭圆C上两上动点，且直线OM、ON的斜率之积等于直线OA、OB的斜率之积，试探求△OMN的面积是否为定值，说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练填空题押题练F组练习卷（解析版） 题型：填空题

    在平面直角坐标系xOy中，直线3x＋4y－5＝0与圆x2＋y2＝4相交于A，B两点，则弦AB的长等于________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练填空题押题练F组练习卷（解析版） 题型：填空题

    已知集合M＝{1,2,3}，N＝{2,3,4}，则M∩N＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练填空题押题练D组练习卷（解析版） 题型：填空题

    设四面体的六条棱的长分别为1,1,1,1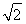，和a且长为a的棱与长为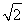的棱异面，则a的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练填空题押题练A组练习卷（解析版） 题型：填空题

    已知函数y＝f(x)(x∈R)上任一点(x0，f(x0))处的切线斜率k＝(x0－3)(x0＋1)2，则该函数的单调递减区间为________．

     

    查看答案和解析>>

    同步练习册答案