
分析 对x讨论,x<1和x≥1时,由一次函数的单调性可得a的范围,再由(2+a)+1≤-a,即可得到所求a的范围.
解答 解:当x<1时,函数f(x)=(2+a)x+1在(-∞,1)递增,
可得2+a>0,即a>-2①,
当x≥1时,函数f(x)=-ax在[1,+∞)递增,可得-a>0,即a<0②,
由f(x)在(-∞,+∞)上为增函数,
可得(2+a)+1≤-a,即a≤-$\frac{3}{2}$③,
由①②③可得,-2<a≤-$\frac{3}{2}$,
故答案为:(-2,-$\frac{3}{2}$].
点评 本题考查分段函数的应用:判断函数的单调性,注意函数在分界点的情况,考查运算能力,属于中档题和易错题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
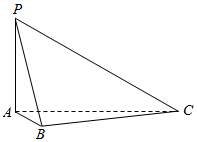 如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC.
如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com