
分析 (1)按照x≤-1,-1<x≤2,x>2三种情况进行讨论,去掉绝对值符号可解不等式,注意三种情况要对x的范围取并集;
(Ⅱ)f(x)≥3即|x-2|+2|x-a|≥3,求出f(x)的最小值是a+2,得到a+2≥3,解出即可.
解答 解:(1)当a=1时,f(x)=|x-2|+2|x+1|,
①当x≤-1时,f(x)=2-x-2(x+1)=-3x,
由f(x)>8,得-3x>8,解得x<-$\frac{8}{3}$;
②-1<x≤2时,f(x)=2-x+2(x+1)=x+4,
由f(x)>8,得x>4,
∴此时不等式无解;
③当x>2时,f(x)=x-2+2(x+1)=3x,
由f(x)>8,得3x>8,解得x>$\frac{8}{3}$;
综上,不等式f(x)>3的解集为(-∞,-$\frac{8}{3}$)∪($\frac{8}{3}$,+∞).
(2)∵a>0,∴-a<0<2,
f(x)=|x-2|+2|x+a|=$\left\{\begin{array}{l}{-3x+2-2a,x≤-a}\\{x+2a+2,-a<x<2}\\{3x-2+2a,x≥2}\end{array}\right.$,
∴f(x)min=f(-a)=a+2,
f(x)≥3即a+2≥3,解得:a≥1.
点评 对于含有绝对值的题目,本身就是分类的,问题的提出已包含了分类的原因.分类讨论是一种逻辑方法,是一种重要的数学思想,同时也是一种重要的解题策略,它体现了化整为零、积零为整的思想与归类整理的方法,在高考试题中占有重要的位置.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
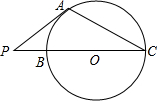 如图,已知PA与圆O相切于点A,经过圆心O的割线PBC交圆O于点B,C,AC=AP,则$\frac{PC}{AC}$的值为( )
如图,已知PA与圆O相切于点A,经过圆心O的割线PBC交圆O于点B,C,AC=AP,则$\frac{PC}{AC}$的值为( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com