
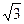 sin
sin xcos
xcos x-cos2
x-cos2 x,其中
x,其中 为使函数f(x)能在x=
为使函数f(x)能在x=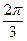 时取得最大值时的最小正整数.
时取得最大值时的最小正整数. 的值;
的值; a、b、c满足b2=ac,且边b所对的角
a、b、c满足b2=ac,且边b所对的角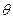 的取值集合为A,当x
的取值集合为A,当x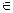 A时,求函数f(x)的值域.
A时,求函数f(x)的值域.科目:高中数学 来源:不详 题型:解答题
 (米)随着时间
(米)随着时间 而周期性变化,每天各时刻
而周期性变化,每天各时刻 的浪高数据的平均值如下表:
的浪高数据的平均值如下表: | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
 | 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.5 | 1.0 |
 中选择一个合适的函数模型,并求出该拟合模型的解析式;
中选择一个合适的函数模型,并求出该拟合模型的解析式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (其中
(其中 )的图象与x轴在原点右侧的第一个交点为N(6,0),又
)的图象与x轴在原点右侧的第一个交点为N(6,0),又 (1)求这个函数解析式(2)设关于x的方程
(1)求这个函数解析式(2)设关于x的方程 在[0,8]内有两个不同根
在[0,8]内有两个不同根 ,求
,求 的值及k的取值范围。
的值及k的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的图象先向左平移
的图象先向左平移 个单位,然后向上平移1个单位,得到函数
个单位,然后向上平移1个单位,得到函数 的图象,则
的图象,则 是( )
是( ) A.- | B.2cosx | C.2sinx | D.-2cosx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com