练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设AB是圆x2+y2=1的一条直径，以AB为直角边、B为直角顶点,逆时针方向作等腰直角三角形ABC.当AB变动时，求C点的轨迹.

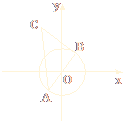
    所求轨迹是以原点为圆心，为半径的圆.


    解析:

    解法一:(参数法)取∠xOB=θ为参数，则B(cosθ,sinθ),

    于是，(x－cosθ)2+(y－sinθ)2=4.

    =－cotθ,消去θ得x2+y2=5.

    故所求轨迹是以原点为圆心，为半径的圆.

    解法二:(相关点法)设C(x,y)、B(x0,y0),

    当x0、y0≠0时，

    则(x－x0)2+(y－y0)2=4.

    ·=－1.由x02+y02=1消去x0、y0得轨迹方程.显然当x0=0或y0=0时，方程也适合.

    解法三:(几何法)连结CO，因为|OC|2=|OB|2+|AB|2=5为定值，故其轨迹为圆.

    评析:求轨迹的方法很多，注意合理选取，参数法求轨迹方程是常用方法之一，常用到的参数有斜率、点的坐标、长度、夹角等.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设点P是圆x2+y2=4上任意一点，由点P向x轴作垂线PP0，垂足为Po，且
    MP0
    =
    		3
    2
    pp0
    ．
    （Ⅰ）求点M的轨迹C的方程；
    （Ⅱ）设直线l：y=kx+m（m≠0）与（Ⅰ）中的轨迹C交于不同的两点A，B．
    （1）若直线OA，AB，OB的斜率成等比数列，求实数m的取值范围；
    （2）若以AB为直径的圆过曲线C与x轴正半轴的交点Q，求证：直线l过定点（Q点除外），并求出该定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源：训练必修二数学人教A版 人教A版 题型：044

    设AB是圆x2＋y2＝1的一条直径，以AB为直角边、B为直角顶点，逆时针方向作等腰Rt△ABC．当AB变动时，求C点的轨迹．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖北省武汉市武昌区高三上学期期末调研测试理科数学试卷（解析版） 题型：解答题

    （本题满分13分）

    设点P是圆x2 +y2 =4上任意一点，由点P向x轴作垂线PP0，垂足为Po，且．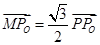

    （Ⅰ）求点M的轨迹C的方程；

    （Ⅱ）设直线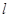：y=kx+m(m≠0)与（Ⅰ）中的轨迹C交于不同的两点A，B．

    （1）若直线OA，AB，OB的斜率成等比数列，求实数m的取值范围；

    （2）若以AB为直径的圆过曲线C与x轴正半轴的交点Q，求证：直线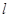过定点(Q点除外)，并求出该定点的坐标．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

         设点P是圆x2 +y2 =4上任意一点，由点P向x轴作垂线PP0，垂足为Po，且．

        （Ⅰ）求点M的轨迹C的方程；

        （Ⅱ）设直线：y=kx+m(m≠0)与（Ⅰ）中的轨迹C交于不同的两点A，B．

            （1）若直线OA，AB，OB的斜率成等比数列，求实数m的取值范围；

            （2）若以AB为直径的圆过曲线C与x轴正半轴的交点Q，求证：直线过定点(Q点除外)，并求出该定点的坐标．

    查看答案和解析>>

    同步练习册答案