
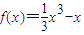 .
.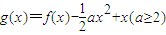 ,求曲线y=g(x)在(1,g(1))处的切线与两坐标轴围成的三角形面积的最小值.
,求曲线y=g(x)在(1,g(1))处的切线与两坐标轴围成的三角形面积的最小值.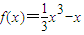 ,知f′(x)=x2-1,令f′(x)=0,得x=±1,由此得到f(x)在x∈[-2,-1]上的最大值为f(3)=6,故要使得不等式f(x)<k-2005对于x∈[-2,3]恒成立,等价于6<k-2005恒成立,由此能求出最小的正整数k.
,知f′(x)=x2-1,令f′(x)=0,得x=±1,由此得到f(x)在x∈[-2,-1]上的最大值为f(3)=6,故要使得不等式f(x)<k-2005对于x∈[-2,3]恒成立,等价于6<k-2005恒成立,由此能求出最小的正整数k.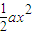 +x=
+x=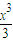 -
-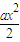 ,知g′(x)=x2-ax,g(1)=
,知g′(x)=x2-ax,g(1)= ,故切线方程为y-(
,故切线方程为y-( -
-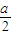 )=(1-a)(x-1),与坐标轴的交点为(0,
)=(1-a)(x-1),与坐标轴的交点为(0, -
-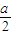 ),(
),(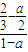 ,0),由此能求出三角形面积的最小值.
,0),由此能求出三角形面积的最小值.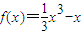 ,
, ×(-2)3-(-2)=-
×(-2)3-(-2)=- ,f(-1)=-
,f(-1)=- +1=
+1= .
. -1=-
-1=- ,
,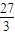 -3=6.
-3=6. +x=
+x=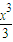 -
-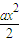 ,
,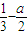 ,
, -
- )=(1-a)(x-1),
)=(1-a)(x-1), -a=0,与坐标轴的交点为(0,
-a=0,与坐标轴的交点为(0, -
-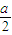 ),(
),(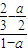 ,0),
,0), -
- <0,
<0,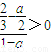 ,
,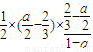 =
=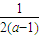 (
(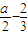 )2,
)2,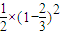 =
= .
.

 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:2007年江苏省连云港市东海高级中学高考数学仿真试卷(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省高三第一次月考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数 .
.
(1)若函数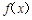 在(
在(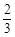 ,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
(2)是否存在正整数a,使得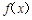 在(
在(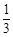 ,
, )上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
)上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年吉林省高三下学期期初考试文科数学试卷 题型:解答题
(本小题满分12分)已知函数 .
.
(1)若把 图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再把所得图象向右平移
图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再把所得图象向右平移 ,得到函数
,得到函数 的图象,写出
的图象,写出 的函数解析式;
的函数解析式;
(2)若 且
且 与
与 共线,求
共线,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010年福建省四地六校高二下学期第二次联考数学(文科)试题 题型:解答题
(本小题满分14分)已知函数 ,
, 
(1)若函数 在
在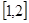 上是减函数,求实数
上是减函数,求实数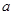 的取值范围;
的取值范围;
(2)令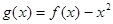 ,是否存在实数
,是否存在实数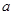 ,当
,当
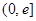 (
(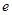 是自然常数)时,函数
是自然常数)时,函数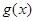 的最小值是3,若存在,求出
的最小值是3,若存在,求出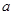 的值;若不存在,说明理由。
的值;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2012届山东省高二下学期期末考试数学(理) 题型:解答题
已知函数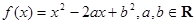 .
.
(1)若从集合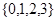 中任取一个元素
中任取一个元素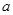 ,从集合
,从集合 中任取一个元素
中任取一个元素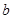 ,求方程
,求方程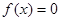 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若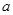 是从区间
是从区间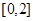 中任取的一个数,
中任取的一个数,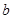 是从区间
是从区间 中任取的一个数,求方程
中任取的一个数,求方程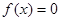 没有实根的概率.
没有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com