
如图椭圆C的方程为![]() ,A是椭圆C的短轴左顶点,过A点作斜率为﹣1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为
,A是椭圆C的短轴左顶点,过A点作斜率为﹣1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为![]() .
.
(1)求椭圆C的方程;
(2)在直线AB上求一点M,使得以椭圆C的焦点为焦点,且过M的双曲线E的实轴最长,并求此双曲线E的方程.

解答: 解:(1)![]() ,又∠PAB=45°,AP=PB,故AP=BP=3.
,又∠PAB=45°,AP=PB,故AP=BP=3.
∵P(1,0),A(﹣2,0),B(1,﹣3)
∴b=2,将B(1,﹣3)代入椭圆得: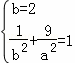 得a2=12,
得a2=12,
所求椭圆方程为![]() .
.
(2)设椭圆C的焦点为F1,F2,
则易知F1(0,﹣![]() )F2(0,
)F2(0,![]() ),
),
直线AB的方程为:x+y+2=0,因为M在双曲线E上,要双曲线E的实轴最大,只须||MF1|﹣|MF2||最大,设F1(0,﹣![]() )关于直线AB的对称点为F1'(
)关于直线AB的对称点为F1'(![]() ﹣2,﹣2),则直线F2F1′与直线的交点为所求M,
﹣2,﹣2),则直线F2F1′与直线的交点为所求M,
因为F2F1′的方程为:![]() ,联立
,联立![]() 得M(1,﹣3)
得M(1,﹣3)
又2a′=||MF1|﹣|MF2||=||MF1'|﹣|MF2||≤|F2F1'|
=![]() =2
=2![]() ,故
,故![]() ,
,
故所求双曲线方程为:![]()



科目:高中数学 来源: 题型:
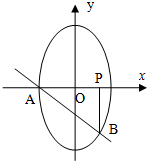 如图椭圆C的方程为
如图椭圆C的方程为| y2 |
| a2 |
| x2 |
| b2 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:湖南省2007届高三十校联考第一次考试-文科数学 题型:038
如图椭圆C的方程为![]() ,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为
,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为![]() .
.
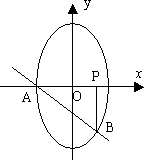
(1)求椭圆C的方程;
(2)在直线AB上求一点M,使得以椭圆C的焦点为焦点,且过M的双曲线E的实轴最长,并求此双曲线E的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2013学年湖北省荆门市高二(下)期末数学试卷(文科)(解析版) 题型:解答题
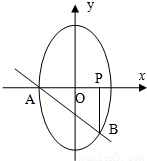 如图椭圆C的方程为
如图椭圆C的方程为 ,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为
,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为 .
.查看答案和解析>>
科目:高中数学 来源:2006-2007学年湖南省十校高三3月联考数学试卷(文科)(解析版) 题型:解答题
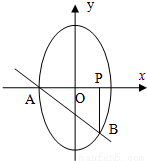 如图椭圆C的方程为
如图椭圆C的方程为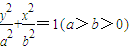 ,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为
,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com