
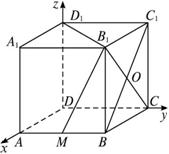
(1)求CD与平面ACD1所成的角;
(2)求证:平面B1CD1⊥平面B1CM;
(3)求点A1到平面B1CM的距离.
(1)解法一:由于∠D1CD=∠ACD,
∴CD在平面ACD1上的射影是∠ACD1的角平分线.
∴由cos45°=cos30°cosθ,得cosθ=![]() ,
,
即CD与平面ACD1所成的角为θ=arccos![]() .
.
解法二:作、证、算得θ=arccos![]() .
.
解法三:建立图示空间直角坐标系,cos〈![]() ,
,![]() 〉=
〉=![]() ,
,

∴θ=![]() -arccos
-arccos![]() .
.
(2)证法一:易得二面角BB1CD1的平面角∠BOD1=90°,
∴平面B1CD1⊥平面B1CM.
证法二:由AC1⊥平面B1CD1,MO∥AC1,可得证.
证法三:求出平面B1CM的一个法向量n=(-1,-2,1),
由n·![]() =0(∵
=0(∵![]() ⊥平面B1CD1),
⊥平面B1CD1),
从而得到平面B1CM⊥平面B1CD1.
(3)解法一:由![]() =
=![]() ,
,
得点A1到平面B1CM的距离d=![]() .
.
解法二:用向量求d=![]() =
=![]() .
.


科目:高中数学 来源: 题型:
 如图正方体ABCD-A1B1C1D1的棱长为1,点M是棱AA1的中点,点O是BD1的中点,求证:OM是异面直线AA1,BD1的公垂线,并求OM的长.
如图正方体ABCD-A1B1C1D1的棱长为1,点M是棱AA1的中点,点O是BD1的中点,求证:OM是异面直线AA1,BD1的公垂线,并求OM的长.查看答案和解析>>
科目:高中数学 来源: 题型:
 (文)如图正方体ABCD-A1B1C1D1,在它的12条棱及12条面的对角线所在的直线中,选取若干条直线确定平面,在所有的这些平面中:
(文)如图正方体ABCD-A1B1C1D1,在它的12条棱及12条面的对角线所在的直线中,选取若干条直线确定平面,在所有的这些平面中:查看答案和解析>>
科目:高中数学 来源: 题型:
 甲.如图1,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=
甲.如图1,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=| 2 |
| AE |
| D1B |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com