
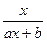 (a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。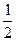 (2)
(2)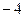 (3)3
(3)3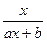 =x的解,
=x的解,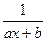 =1无解或有解为0,若无解,则ax+b=1无解,得a=0,矛盾,若有解为0,则b=1,所以a=
=1无解或有解为0,若无解,则ax+b=1无解,得a=0,矛盾,若有解为0,则b=1,所以a=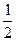 。
。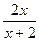 ,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,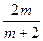 =4,m= –4(必要性),
=4,m= –4(必要性),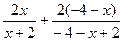 =……=4成立(充分性) ,所以存在常数m= –4,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
=……=4成立(充分性) ,所以存在常数m= –4,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,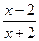 )2,设x+2=t,t≠0,
)2,设x+2=t,t≠0,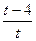 )2=t2+2t+2–
)2=t2+2t+2–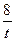 +
+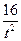 =(t2+
=(t2+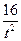 )+2(t–
)+2(t–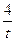 )+2=(t–
)+2=(t–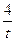 )2+2(t–
)2+2(t–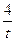 )+10
)+10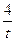 +1)2+9,所以当t–
+1)2+9,所以当t–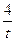 +1=0时即t=
+1=0时即t=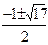 ,也就是x=
,也就是x=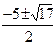 时,|AP| min =" 3" 。
时,|AP| min =" 3" 。

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
 则每两客车营运多少年,其运营的年平均利润最大 ( )
则每两客车营运多少年,其运营的年平均利润最大 ( )| A.3 | B.4 | C.5 | D.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com