
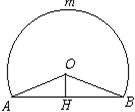
 张堰镇为了搞好小区建设美化家园,在新建小区修建一个绿色扇形花坛如图,已知扇形OAB的中心角为4弧度,其面积为2平方米,求扇形的周长和弦AB的长.
张堰镇为了搞好小区建设美化家园,在新建小区修建一个绿色扇形花坛如图,已知扇形OAB的中心角为4弧度,其面积为2平方米,求扇形的周长和弦AB的长.科目:高中数学 来源: 题型:
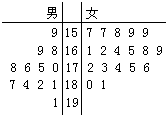 第26届世界大学生夏季运动会将于2011年8月12日到23日在中国广东举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.若从所有“高个子”
第26届世界大学生夏季运动会将于2011年8月12日到23日在中国广东举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.若从所有“高个子”查看答案和解析>>
科目:高中数学 来源: 题型:
| n(ad-bc)2 | (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
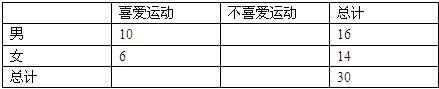
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
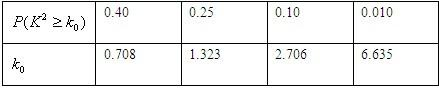
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com