
分析 (1)利用等差数列与等比数列的通项公式及其求和公式即可得出.
(2)an<an+1,由(1)知an=2n-1,${b_n}={2^{n-1}}$.利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
∵a1=b1=1,且b3S3=36,b2S2=8(n∈N*).
∴$\left\{\begin{array}{l}{{q}^{2}(3+3d)=36}\\{q(2+d)=8}\end{array}\right.$,解得$\left\{\begin{array}{l}{d=2}\\{q=2}\end{array}\right.$或$\left\{\begin{array}{l}{d=-\frac{2}{3}}\\{q=6}\end{array}\right.$.
∴an=2n-1,bn=2n-1;或an=1-$\frac{2}{3}$(n-1)=$\frac{5-2n}{3}$,bn=6n-1.
(2)∵an<an+1,∴由(1)知an=2n-1,${b_n}={2^{n-1}}$.
∴${T_n}=1+3×2+5×{2^2}+…+(2n-1)×{2^{n-1}}$.
∴2Tn=2+3×22+5×23+…+(2n-3)×2n-1+(2n-1)×2n,
∴-Tn=1+2(2+22+…+2n-1)-(2n-1)×2n=1+$\frac{2×({2}^{n-1}-1)}{2-1}$-(2n-1)×2n=-(2n-3)×2n-3.
∴Tn=(2n-3)×2n+3.(n∈N*)
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
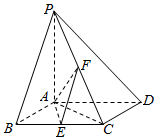 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,1] | B. | (-∞,$\frac{1}{2}$]∪[1,+∞) | C. | [-$\frac{1}{2}$,1] | D. | (-∞,-$\frac{1}{2}$)∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N=U | B. | M∩N=N | C. | M∩(∁UN)=∅ | D. | M⊆∁UN |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{3π}{4}$个单位,再将所得图象上每点纵坐标不变,横坐标变为原来的2倍 | |
| B. | 向左平移$\frac{3π}{4}$个单位,再将所得图象上每点纵坐标不变,横坐标变为原来的2倍 | |
| C. | 每点纵坐标不变,横坐标变为原来的2倍,再将所得图象向右平移$\frac{3π}{4}$个单位 | |
| D. | 每点纵坐标不变,横坐标变为原来的2倍,再将所得图象向左平移$\frac{3π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com