
分析 先确定对称轴属于区间[-1,1],函数f(x)有唯一零点时△=0确定一个值;当△大于零0时,分开口向上和向下两种情况讨论.
解答 解:∵f(x)=3ax2-2ax+1是二次函数则a≠0,对称轴为x=$\frac{1}{3}$∈[-1,1];
①△=0时4a2-12a=0∴a=3或a=0(舍去);
②△>0时,
当a>0时开口向上,∴$\left\{\begin{array}{l}f(-1)≥0\\ f(1)<0\end{array}\right.$;
∴$\left\{\begin{array}{l}a≥-\frac{1}{5}\\ a<-1\end{array}\right.$∴无解;
当a<0时开口向下,∴$\left\{\begin{array}{l}f(-1)≤0\\ f(1)>0\end{array}\right.$,
∴$\left\{\begin{array}{l}a≤-\frac{1}{5}\\ a>-1\end{array}\right.$,∴-1<a≤-$\frac{1}{5}$,
实数a的取值范围:{3}或{a|-1<a≤-$\frac{1}{5}$}.
点评 本题主要考查函数零点问题.注意零点不是点,是函数f(x)=0时,x的值.


科目:高中数学 来源: 题型:解答题
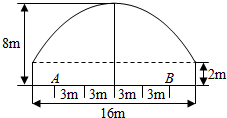 有一隧道,内设双行线公路,同方向有两个车道(共有四个车道),每个车道宽为3m,此隧道的截面由一个长方形和一抛物线构成.如图所示,隧道高8m,宽16m,为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方面上高度之差至少为0.25m,靠近中轴线的车道为快车道,两侧的车道为慢车道,求车辆通过隧道时,慢车道的限制高度(用分数表示).
有一隧道,内设双行线公路,同方向有两个车道(共有四个车道),每个车道宽为3m,此隧道的截面由一个长方形和一抛物线构成.如图所示,隧道高8m,宽16m,为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方面上高度之差至少为0.25m,靠近中轴线的车道为快车道,两侧的车道为慢车道,求车辆通过隧道时,慢车道的限制高度(用分数表示).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,-4] | B. | [-5,-4] | C. | (-∞,-4) | D. | (-∞,-4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c2=a2+b2+2abcosC | B. | c2=a2+b2-2abcosC | ||
| C. | c2=a2+b2+2absinC | D. | c2=a2+b2-2absinC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1,0) | B. | (0,-1,0) | C. | (0,0,3) | D. | (0,0,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
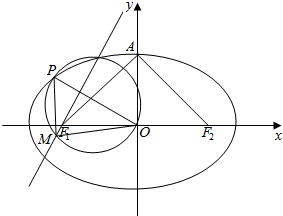 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,点A是椭圆的上顶点,△AF1F2为等腰直角三角形,点P为椭圆任意一点,且|PF1|的最小值为$\sqrt{2}$-1;以OP为直径作圆E,过F1作OP的垂线交圆E于M.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,点A是椭圆的上顶点,△AF1F2为等腰直角三角形,点P为椭圆任意一点,且|PF1|的最小值为$\sqrt{2}$-1;以OP为直径作圆E,过F1作OP的垂线交圆E于M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com