
已知函数 在
在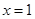 与
与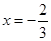 时,都取得极值.
时,都取得极值.
(1)求 的值;
的值;
(2)若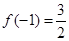 ,求
,求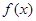 的单调区间和极值;
的单调区间和极值;
(3)若对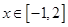 都有
都有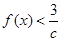 恒成立,求
恒成立,求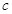 的取值范围.
的取值范围.
(1)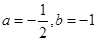 ;(2)f (x)的递增区间为(-∞,-
;(2)f (x)的递增区间为(-∞,-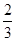 ),及(1,+∞),递减区间为(-
),及(1,+∞),递减区间为(-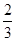 ,1),当x=-
,1),当x=-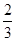 时,f (x)有极大值,f (-
时,f (x)有极大值,f (-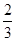 )=
)=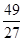 ;当x=1时,f (x)有极小值,f (1)=-
;当x=1时,f (x)有极小值,f (1)=-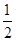 ;(3)
;(3)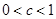 或
或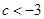 .
.
【解析】
试题分析:(1)函数的极值点是使导数等于0的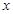 的值,因此本题中一定有
的值,因此本题中一定有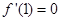 和
和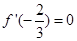 ,由此可解出
,由此可解出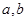 的值;(2)再由
的值;(2)再由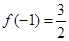 可求出
可求出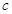 ,而求单调区间,很显然是解不等式
,而求单调区间,很显然是解不等式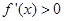 (得增区间)或
(得增区间)或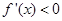 (得减区间),然后可得相应的极大值和极小值;(3)
(得减区间),然后可得相应的极大值和极小值;(3)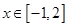 不等式
不等式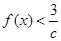 恒成立,实际上就是当
恒成立,实际上就是当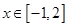 时
时 的最大值小于
的最大值小于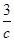 ,因此问题转化为先求
,因此问题转化为先求 在
在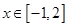 上的最大值
上的最大值 ,然后再解不等式
,然后再解不等式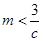 即可.
即可.
试题解析:(1)f ′(x)=3x2+2a x+b=0.
由题设,x=1,x=-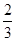 为f ′(x)=0的解.
为f ′(x)=0的解.
-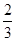 a=1-
a=1-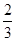 ,
,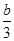 =1×(-
=1×(-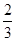 ).∴a=-
).∴a=-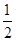 ,b=-2
3分
,b=-2
3分
经检验得:这时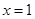 与
与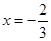 都是极值点. …4分
都是极值点. …4分
(2)f (x)=x3-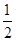 x2-2 x+c,由f (-1)=-1-
x2-2 x+c,由f (-1)=-1-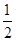 +2+c=
+2+c= ,c=1.
,c=1.
∴f (x)=x3-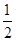 x2-2 x+1.
x2-2 x+1.

∴f(x)的递增区间为(-∞,-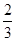 ),及(1,+∞),递减区间为(-
),及(1,+∞),递减区间为(-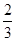 ,1).
,1).
当x=-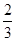 时,f (x)有极大值,f (-
时,f (x)有极大值,f (-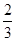 )=
)=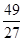 ;
;
当x=1时,f (x)有极小值,f (1)=-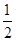 …8分
…8分
(3)由(1)得,f′(x)=(x-1)(3x+2),f (x)=x3-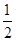 x2-2 x+c,
x2-2 x+c,
f (x)在[-1,-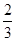
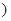 及(1,2]上递增,在(-
及(1,2]上递增,在(-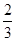 ,1)递减.
,1)递减.
而f (-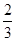 )=-
)=-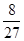 -
- +
+ +c=c+
+c=c+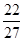 .f (2)=8-2-4+c=c+2.
.f (2)=8-2-4+c=c+2.
∴ f (x)在[-1,2]上的最大值为c+2.∴ 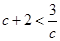 ,∴
,∴ 
∴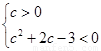 或
或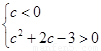 ∴
∴ 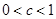 或
或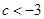 12分
12分
考点:(1)导数与极值;(2)导数与单调区间;(3)不等式恒成立问题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2013届辽宁盘锦二中高二下学期月考理科数学试卷(解析版) 题型:解答题
(满分12分) 已知函数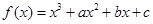 在
在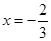 与
与 时都取得极值
时都取得极值
(1)求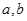 的值与函数
的值与函数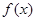 的单调区间
的单调区间
(2)若对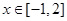 ,不等式
,不等式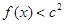 恒成立,求c的取值范围
恒成立,求c的取值范围
查看答案和解析>>
科目:高中数学 来源:2012届江苏省高三数学国庆作业二(文科) 题型:解答题
已知函数 在
在 与
与 时,都取得极值。
时,都取得极值。
(1)求 的值;
的值;
(2)若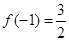 ,求
,求 的单调区间和极值;
的单调区间和极值;
(3)若对 都有
都有 恒成立,求
恒成立,求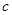 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com